"Золотая пропорция"

Обратимся вначале к изобразительному искусству, которое в значительной мере опирается на пропорции и, можно сказать, держится ими.

Уже древние хорошо понимали, что в основе совершенных творений искусства лежат математически безупречные соотношения частей и элементов. Недаром же всю греческую архитектуру считают внешним выражением учения Эвклида, а древнеегипетские пирамиды - "немым трактатом" по геометрии. Следовательно, уже тогда математика служила своего рода "грамматикой архитектуры". Ею она осталась и теперь.

Образцы недосягаемых творений созданы также мастерами античной скульптуры. И первую роль в этом сыграло то, что были тщательно изучены пропорции человеческого тела.

Природа сотворила человека так, что его лицо от подбородка до верхней границы лба составляет 1/10 всей длины тела. Такую же 1/10 его доли имеет ладонь. Рука до локтя как и ширина груди, равна 1/4 тела, а длина ступни - 1/6.

Аналогично и остальные части обладают свойственными им гармоничными пропорциями. Так, античные скульпторы считались с правилом, по которому длина тела от кончиков ног до макушки соответствует длине раскинутых рук. Поэтому распростертая фигура напоминает знак X. Проведем мысленный эксперимент. Уложим на землю человека, который пусть свободно раскинет руки и ноги. Затем возьмем большой циркуль. Если одну ножку его водрузим в центр живота, то другая опишет круг, который пройдет как раз по кончикам пальцев рук и ног.

Таким образом, что касается человеческого тела, то в древности было все изучено и все измерено, оставалось только воплощать найденные пропорции в художественные формы. Мастера той далекой поры умели делать это с непревзойденным успехом, создавая отличные скульптурные произведения.

Характерно, что соотношения частей человеческого тела стали тогда применять также в архитектуре. Согласно легенде дорический ордер (вид колонны) возник следующим образом. Как уже отмечалось, длина ступни (точнее сказать, мужской ступни) равна 1/6 человеческого роста. Этой мерой и воспользовались при возведении зданий. Толщину колонны в основании откладывали 6 раз, что и определяло ее высоту.

Практиковалось также другое соотношение. В частности, при постройке храма в честь богини Дианы взяли пропорцию, которой отличаются стройные женщины. В этом случае толщина колонны составляла лишь 1/8 ее высоты. Благодаря этому колонна казалась выше, чем она была на самом деле, и как раз за счет уменьшения толщины. В архитектуру так и вошли оба вида колонн, сохраняющие одна мужскую, другая женскую пропорции в отношениях между основанием и высотой.

Красивейшим проявлением гармонии является так называемое "золотое сечение". Это особое разбиение отрезка, когда образуется изящная пропорция полученных частей. Настолько изящная, что математики Возрождения называли ее "божественной", а И. Кеплер писал: "Геометрия обладает двумя великими сокровищами - это теорема Пифагора, вторая - деление отрезка в среднем и крайнем соотношении. Первое можно сравнить с мерой золота, второе можно назвать драгоценным камнем".

Так что же представляет собой это сечение? Здесь вновь придется прибегнуть к языку, суровому и даже безжалостному ко всякого рода украшениям стиля, - к языку математики. Точка делит отрезок в среднем и крайнем отношении (то есть образует "золотое сечение"), если отношение большей части отрезка к меньшей равно отношению всего отрезка к его большей части. На предлагаемом рисунке точка В как раз и разделит отрезок АС так, что АВ : ВС = АС : АВ.

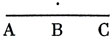
Формула

Действительно, в формах, созданных по норме "золотой пропорции" или деления отрезка в среднем и крайнем отношении, есть что-то привлекательное. Как и любое яркое свойство, оно постоянно притягивало к себе внимание. Итальянский математик XV века Л. Пачиоли приводит массу качеств "золотого сечения". "Оно производит на нас, - пишет Л. Пачиоли, - действие, во-первых, существенное, во-вторых, особое, в-третьих, невыразимое, в-четвертых, неизъяснимое, в-пятых, в-шестых..." и т. д. Наконец, он сказал, "в-тринадцатых, достойнейшее", затем остановился и начал возносить "Тайную вечерю" Л. да Винчи как образец художественного совершенства, достигнутого на основе учета точных пропорций.

Позднее установили, что "золотое сечение" составляет структуру многих природных тел. О многих говорить не будем, а вот про человека сказать стоит. Оказывается, талия делит совершенную человеческую фигуру как раз в отношении "золотой пропорции". Интересно, что у новорожденных талия приходится на середину тела, то есть разделяет его как раз пополам. Вообще, эта закономерность деления в крайнем и среднем отношении присуща и отдельным частям человеческой фигуры.

Когда установили, что "золотое сечение" лежит в основе различных природных явлений, его стали применять не только в искусстве, но и в технике, создавая машины, конструкции, строения. Впрочем, техническую деятельность не приходится резко противопоставлять художественной, ибо, как мы попытаемся показать в следующей из глав, одним из показателей надежности механизмов, сооружений и т. п. как раз выступает критерий красоты.

Золотое сечение

А теперь хотелось бы обратиться к теории и практике самих мастеров искусства, посмотреть, как они решают затронутые здесь проблемы связи художественного изобразительного творчества с точной наукой.

В глубине столетий возвышается фигура Л. да Винчи. Его свидетельства тем более значимы, что он, сочетая таланты ученого и живописца, присоединил к ним способность еще и теоретика искусства, стремившегося выяснить естественнонаучные основания красоты, установить точные законы, по которым создается прекрасное.

На первое место выходит у него математика. Он подчеркивает, что художник обязан прежде всего знать эту науку, уметь владеть ею, чтобы постигать гармонию, поскольку она покоится на пропорции, мере и числе. Выясняя причины действия на зрителя живописи, которую он почитал вершиной художественного, Л. да Винчи ставит "виной" то, что первым ее основанием является точка, вторым - линия, третьим - поверхность, четвертым - тело, которое одевается этой поверхностью.

Им разработаны также математические законы перспективы, принципы передачи объемности реальных предметов на плоскости, принципы, так сказать, "перевода" событий трехмерного мира в двухмерный. Короче, он подходит к живописи с позиции строгих геометрических требований. Потому она и представлялась ему образцом совершенства не только в искусстве, но и в науке.

Таким образом, Л. да Винчи является нам человеком, глубоко осознавшим роль математики в изобразительном творчестве. Он не допускал и мысли, что к художественным воплощениям натуры можно приступать, обходя стороной точную науку, не считаясь с ее количественными предписаниями. Поэтому с большим сожалением отмечал, как иные служители искусства из-за невежества неспособны понять научных оснований живописи. Не потому ли они так и остались позади этих оснований?

Столь же настойчиво искал математическую опору рисунка художник немецкого Возрождения А. Дюрер. Он вел переписку с видными учеными (иных знал по личным встречам), обсуждая проблемы, возникающие в точках касания математики и живописи. Особая дружба связывала его с уже упоминавшимся Л. Пачиоли. Словом, А. Дюрер вполне заслужил характеристику "прирожденного геометра", которую ему выдают специалисты.

Как и Л. да Винчи, А. Дюрер с сожалением отмечает, что в Германии многие "живописцы... не изучают науки измерения, без которой невозможно сделаться настоящим мастером". Он полагает непреложным в изображении человеческих фигур придерживаться четких правил, продиктованных природой. А правила эти таковы, пишет художник, что размеры груди, лица, головы и т. д. составляют непроизвольную, но строго определенную часть длины тела. Пропорции, которые он указывает, те же, что называли в свое время древние.

Стоит обратить внимание и на П. Учелло, итальянского живописца этой же поры, примечательного тем, что всю творческую жизнь посвятил изучению математических законов перспективы. И пусть как исполнитель он не достиг высот, занимаемых Л. да Винчи или А. Дюрером, его след в разработке теории вопроса остался.

Мы увидели ряд выдающихся мастеров, познакомились с их мнениями по поводу научного фундамента искусства и убедились, что проникнуть в тайны художественности им помогло знание методов точных наук. Они отыскали ряд математических законов, которые управляют работой живописца или скульптора в минуты, когда создается прекрасное. По мнению специалистов, у таких художников, как JI. да Винчи, А. Дюрер, а из более поздних Микеланджело, Х. Рембрандт, подготовка в области математики была выше, чем у многих современных им естествоиспытателей.

Однако пусть у читателя не образуется убеждение, будто все это в далеком прошлом (когда действительно пришлось разрабатывать математические основы живописи), но что, мол, не является уже обязательной нормой для художников, скажем, XIX или нынешнего столетия. Можно безоговорочно утверждать, что во все времена одно из составляющих успеха изобразительного творчества - в обязательном общении с точной наукой.

В этой связи характерен эпизод, имевший место в творческой биографии выдающегося русского художника В. Сурикова.

Работая над картиной "Боярыня Морозова", он споткнулся на том, как создать у зрителя иллюзию движения саней, в которых везут боярыню. Чутье подсказывало, что сани "поедут", только если полозья поместить на строго определенном расстоянии от рамы. И художник искал его, испытывая разные варианты. То есть, говоря современным ученым языком, моделировал, чтобы определить это единственно точное положение саней. Он записал тогда: "Главное для меня - композиция. Тут есть какой-то твердый неумолимый закон, который можно только... угадать, но который до того непреложен, что каждый прибавляемый или убавляемый вершок холста или лишняя поставленная точка разом меняет всю композицию". А далее В. Суриков поделился особенно важным для настоящего разговора наблюдением. "В движении, - говорит он, - есть живые точки, а есть мертвые. Это настоящая математика. Сидящие в санях фигуры держат их на месте. Надо было найти расстояние от рамы до саней, чтобы пустить их в ход. Чуть меньше расстояние, сани стоят".

Интересно, что, когда картину смотрел Л. Толстой с женой, они посоветовали срезать низ, мотивируя тем, что он не нужен, мешает. На это В. Суриков возразил: "А там ничего убавить нельзя - сани не поедут".

Высокое значение математики для изобразительного искусства демонстрирует современный голландский мастер М. Эшер, который счастливо соединил в себе ученого и художника. Он эстетически ярко отобразил в рисунках геометрию пространства. Несмотря на то что из-под его руки выходили все же произведения искусства, М. Эшер явно тяготел и к точной науке. "Я часто ощущаю, - писал он, - большую близость к математике, чем к коллегам-художникам".

Одним словом, если подвести сказанному итог, есть основания вслед за многими теоретиками и практиками искусства признать, что ни один живописец не может писать, не зная геометрии. Вместе с тем приходится согласиться и с другим. Далеко не каждый из живописцев, в том числе, конечно, и нашего времени, этот древний урок усвоил. Очевидно, неудачи, которые их постигают, в значительной мере обусловлены как раз неумением или нежеланием пользоваться орудиями точного расчета - циркулем, угломером и числом.

Теперь мы намерены перейти к математическим основам других видов художественного творчества.