ГЛАВА 15. ВОЛНОВАЯ МЕХАНИКА

НОВЫЕ КВАНТОВОМЕХАНИЧЕСКИЕ ТЕОРИИ

1. РАСПРОСТРАНЕНИЕ СТАТИСТИЧЕСКОГО ЗАКОНА РАДИОАКТИВНОСТИ НА ИЗЛУЧЕНИЕ

Новый механизм, введенный Бором для рассмотрения испускания и поглощения излучения, освобождал квантовую теорию от ограничений, связанных с использованием линейных осцилляторов или аналогичных частных типов систем. Поэтому возникла необходимость вывести формулу излучения черного тела на базе этих новых гипотез.

Разрешением этой проблемы занялся Альберт Эйнштейн, с интересом следивший за работами Бора и с особым сочувствием принявший принцип соответствия, казавшийся многим прелюдией к возможному включению квантовой теории в классическую механику. В 1917г. появилась знаменитая работа Эйнштейна, его крупнейший вклад в квантовую теорию, в которой к атому Бора применялся тот же вероятностный подход, что и для закона радиоактивного распада (Работа, которую имеет в виду Льоцци, вышла в 1917 г. (Physik. Zeitschrift, 18, 121), но еще в 1916 г. она была напечатана в Mitt. Phys. Ges. (Zurich), № 18, 47-62. - Прим. перев). Подобно тому как каждый отдельный радиоактивный атом взрывается в некий непредвиденный момент в результате случайного процесса, не имеющего видимой причины, так и переход электрона в атоме совершенно непредвиден и должен изучаться согласно статистическим законам.

Эйнштейн сформулировал эти законы, предположив, что: 1) при наличии поля излучения вероятность электронного перехода, как связанного с излучением, так и связанного с поглощением, в единицу времени пропорциональна интенсивности излучения; 2) даже без внешних возмущений происходит спонтанный переход электронов из состояний с более высокой энергией в состояния с более низкой энергией с вероятностью, пропорциональной числу атомов, находившихся первоначально в возбужденном состоянии. Таким образом, на явления излучения переносится закон радиоактивного распада.

На этой основе, вновь воспроизводя и обобщая свою теорию броуновского движения, Эйнштейн не только получает формулу Планка для излучения черного тела, но рассматривает также в общем виде вопрос об обмене импульсом между атомной системой и излучением и приходит к выводу, что при каждом элементарном процессе излучения должен испускаться импульс величиной hν/c в совершенно случайном направлении. Этот вывод обострял дилемму волна - корпускула, потому что при таком описании процесса излучения исключалась возможность сферических волн. Такие последствия с огорчением отмечает сам Эйнштейн в конце своей работы:

«Эти свойства элементарного процесса делают почти неизбежным создание подлинно квантовой теории излучения. Слабость теории заключается, с одной стороны, в том, что она не приводит нас к более тесному объединению с волновой теорией, и, с другой стороны, в том, что время и направление элементарного процесса предоставляются "случаю"; впрочем, я полностью уверен в надежности выбранного метода» (A. Einstein, Quantentheorie der Strahlung, Physik. Zeitschrift, 18, 128 (1917). (Есть русский перевод: А. Эйнштейн, Собр. научн. трудов, т. III, стр. 406.)).

Стоит особо подчеркнуть этот первый значительный шаг к индетерминистской физике, сделанный Эйнштейном, который сам оставался всю жизнь убежденным детерминистом. Заметим, что, прибегая к статистике, он все же остается в рамках классических законов причинности. В самом деле, согласно Эйнштейну, точный момент перехода электрона в атоме определен законами причинности, зависящими от структурных свойств возбужденного атома, и лишь наше незнание этих законов и их сложность вынуждают нас прибегать к статистическим методам, играющим роль инструмента. Тем не менее остается историческим фактом, что именно Эйнштейн первый перенес статистический метод, применявшийся при изучении радиоактивности, на другие области физики.

2. АНТИТЕЗА ВОЛНА - ЧАСТИЦА

Примерно к 1923 г. в результате изучения фотоэлектрического эффекта, исследований Бора о строении атома, упомянутой выше теории Эйнштейна, открытия эффекта Комптона физики очутились перед необходимостью рассмотреть самым серьезным образом вопрос о дискретной структуре излучения. Число явлений, которые нельзя было уже объяснить, оставаясь в рамках классической оптики, увеличивалось, можно сказать, с каждым днем. Снова опыт сметал границы, установленные теорией.

На протяжении всей своей истории физика не раз оказывалась в положении, когда общепринятых теорий было недостаточно, но физике всегдЯ удавалось выйти из этого положения, выдвинув новую, более общую теорию, способную объяснить одновременно и старые и новые явления. Однако новый кризис носил совершенно иной характер. Новая теория, теория световых квантов, не представлялась более общей, чем волновая, в том смысле, что некоторые явления, отлично объясняемые классической оптикой, никак нельзя было объяснить новой фотонной теорией.

Противоречие волна - частица, которое в годы, последовавшие за первой мировой войной, казалось неразрешимым, часто сравнивали со спором, возникшим в XVIII веке между эмиссионной теорией Ньютона и волновой теорией Гюйгенса. Но это сравнение, пожалуй, не совсем удачно. В XVIII веке каждая из этих двух теорий объясняла более или менее удачно все известные тогда оптические явления; выбор той или иной теории сводился лишь к вопросу о том, какой способ представляется более простым, или же к личным склонностям, чуть ли не к эстетическим взглядам того или иного ученого. Интуиция говорила в пользу теории Ньютона, которая объясняла самым простым и наглядным способом наиболее привычное оптическое явление - прямолинейное распространение света. Те же ученые, которые были склонны пожертвовать по крайней мере частью общепринятых представлений ради большей логической последовательности, предпочитали теорию Гюйгенса. В этой связи показательно, что волновой концепции придерживались в XVIII веке почти исключительно математики: Иоганн Бернулли младший (1710-1790) и Леонард Эйлер.

В XX веке расхождение было уже не между физиками, а в самой физике. Каждый физик вынужден приписывать свету волновую природу, чтобы объяснить определенные явления (например, дифракцию), и корпускулярную природу, чтобы объяснить другие явления (например, фотоэлектрический эффект). Иными словами, как остроумно заметил Уильям Брэгг, каждый физик вынужден по понедельникам, средам и пятницам считать свет состоящим из частиц, а в остальные дни недели - из волн. Лишь при объяснении немногих явлений (например, прямолинейного распространения света, эффекта Допплера и др.) можно с равным успехом следовать как одной, так и другой теории.

Отчаянное усилие спасти классическую оптику, сегодня уже совершенно забытое, но живо обсуждавшееся в 1924-1927 гг., сделал Бор, надеявшийся включить теорию световых квантов в волновую теорию с помощью принципа соответствия или хотя бы перекинуть мост между двумя этими теориями. В своей статье совместно с Крамерсом и Слэтером, опубликованной в 1924 г., Бор выдвигает любопытную гипотезу, согласно которой атомы постоянно испускают все излучения, соответствующие возможным переходам из состояния, в котором они находятся, в другие стационарные состояния. Но эти излучения являются «виртуальными», т. е. не оказывают никакого физического действия. Они становятся реальными только в случаях, определяемых вероятностным законом Эйнштейна. Эта теория среди прочего предполагала, что законы сохранения энергии и импульса не выполняются для единичных процессов, будучи верными лишь в статистическом смысле для совокупности большого числа элементарных процессов. Таким образом, классическая оптика оказывалась спасенной при придании всем физическим законам статистического значения. Сколько бы усилий ни делали физики, чтобы остаться на почве классических теорий, они каждый раз наталкивались на необходимость статистического подхода!

Зоммерфельд так комментировал эту попытку Бора:

«Сейчас еще слишком рано высказывать окончательное суждение по поводу этой теории, но нам кажется, что компромисс между волновой теорией и теорией квантов, которого пытаются достичь с помощью статистического подхода, носит характер искусственного ухищрения. Также не очень подходящим кажется нам введение в физику таких величин, как поле виртуального излучения, которое, согласно гипотезе, не должно быть наблюдаемо. Все это похоже на историю со световым эфиром, который вследствие относительности движения не должен был явно обнаруживаться и в конце концов был вынужден отступить перед научным прогрессом. Мы рассматриваем противоречие между волновой теорией и квантовой теорией как временную загадку и считаем, что для ее разрешения понадобятся глубокие изменения основных понятий электромагнитного поля и, как в теории относительности, даже основных принципов физического знания» (A. Sommerfeld, Uber die letzte Fortschritte der Atomphysik, Scientia, 39, 18 (1926)).

3. ВОЛНА, СОПРЯЖЕННАЯ С ЧАСТИЦЕЙ

Уже за три года до того, как Зоммерфельд написал эти слова, были выдвинуты новые, глубоко революционные понятия, которые пока еще не разрешали противоречия волна - частица, а, напротив, распространяли его не только на фотон, но и на электрон.

Автором этой новой концепции был молодой французский физик Луи де Бройль (род. в 1892 г.), который сразу же после демобилизации в 1919 г. приступил к своим первым работам в частной лаборатории своего брата Мориса де Бройля (1875-1960), открытой для молодых исследователей, желавших посвятить себя изучению спектров рентгеновских лучей и фотоэлектрического эффекта - самым передовым областям физических исследований того времени, в которых Морис де Бройль приобрел большой международный авторитет.

Луи де Бройль

Изучение рентгеновских лучей, естественно, навело Л. де Бройля на серьезные размышления о природе излучения, и в частности о работах Эйнштейна в области световых квантов. Следы этих размышлений можно видеть в двух заметках 1922 г., относящихся к вопросу об излучении черного тела, которые привели молодого физика «к идее, что, может быть, нужно найти общее синтезирующее понятие, которое позволило бы объединить точку зрения волновой теории с точкой зрения корпускулярной».

С удивительной простотой де Бройль так изложил в своей Нобелевской речи поразившую его фантазию аналогию между корпускулярной и волновой теориями, принятыми физикой того времени:

«С одной стороны, теория световых квантов не может быть признана удовлетворительной, потому что она определяет энергию корпускулы света соотношением W=hν, в котором фигурирует частота ν. Но чисто корпускулярная теория не содержит в себе ни одного элемента, который позволил бы определить частоту. Хотя бы по этой причине необходимо в случае света вводить одновременно и идею корпускулы и идею периодичности.

явлениями в физике, при описании которых входили целые числа, были явления интерференции и собственных колебаний» (L. De Вrоglie, Conference Nobel prononcee a Stockholm, le 12 decembre 1929f p. 4, Les Prix Nobel en 1929, Stockholm, 1929).

И вдруг в результате того самого психологического процесса, который он так тонко проанализировал в одном, быть может, автобиографическом отрывке в конце лета 1923 г., произошла, как он говорит,

«своего рода кристаллизация: разум в один момент схватывает с большой ясностью... основные очертания новых понятий, которые незаметно формулировались в нем, и он получает вдруг абсолютную уверенность в том, что применение этих новых понятий позволит разрешить большинство поставленных проблем и прояснить весь вопрос, апеллируя к до сих пор не учитывавшимся аналогиям и соответствиям» (L. De Вrоglie, Continu et discontinu en physique rnoderne, Paris, 1941, p. 82-83).

Возможность синтетической теории, столь неожиданно ему представившаяся, была разработана в его трех знаменитых докладах, представленных Парижской Академии наук. Эти три статьи, которые являются отправной точкой волновой механики, поражают современного читателя не только смелостью идей, но также чрезвычайной простотой использованных в них математических средств, особенно по сравнению со сложными, иногда даже слишком виртуозными математическими теориями физиков-теоретиков.

В соответствии с теорией относительности Л. де Бройль ислодит из предположения, что с каждой частицей с массой покоя (или энергией) m₀ связан волновой процесс с частотой ν₀, так что hν₀=m₀с₂, где h - постоянная Планка, ас - скорость света в пустоте. Иными словами, этот основной постулат означает, что каждая частица материи является местом и источником связанного с ней колебания с частотой, определяемой выше указанным соотношением. Если эта частица находится в движении, то, согласно теории относительности, ее колебание представляется неподвижному наблюдателю в виде волны, движущейся со скоростью большей, чем скорость частицы. Получив этот результат, де Бройль рассматривает равномерное движение электрона по замкнутой траектории и показывает, что квантовые траектории теории Бора - Зоммерфельда могут быть истолкованы как явление резонанса фазовой волны на длине замкнутой траектории. Другими словами, если электрон движется по замкнутой кривой, то волна должна сопровождать его и замыкаться в непрерывное волновое кольцо, так что длина кольца должна быть равна целому числу длин волн, подобно тому как полосы обоев в точности подойдут к стенам комнаты и между ними не будет видно мест склейки только тогда, когда периметр стен комнаты будет вмещать целое число раз рисунок обоев. Поэтому стационарными орбитами будут те, на которых точно 1, 2, 3, ... раза укладывается длина волны, связанной с вращающимся электроном. Расчет показал, что эти орбиты точно совпадают с определяемыми постулатом Бора.

Затем де Бройль применяет свой подход к фотонам и набрасывает в общих чертах теорию явлений интерференции и дифракции света, исходя из того, что распределение фотонов определяется волнами, так что возможны темные области там, где волны, накладываясь друг на друга, взаимно ослабляются.

Новая концепция приводит де Бройля к закону Планка для излучения черного тела. Кроме того, он устанавливает соответствие, ставшее теперь классическим, между принципом наименьшего действия Мопертюи, примененным к движению частицы, и принципом Ферма, примененным к распространению связанной с ней волны. Новая механика объясняла, таким образом, аналогию, на которую указывал еще Гамильтон, а затем и Якоби (см. гл. 8), между классической динамикой частиц и геометрической оптикой, аналогию, которая поражала Л. де Бройля еще в ранней молодости, но которая, однако, вряд ли была, как это сегодня утверждают некоторые, исходным пунктом, вдохновлявшим его исследования.

Три короткие статьи 1923 г. были объединены и включены в его докторскую диссертацию (1924 г.), в которой новая концепция получила более широкое применение. В ней доказывается, например, что новые принципы позволяют количественно объяснить эффект Допплера, отражение от движущегося зеркала и давление излучения, приводя к тем формулам, которые дает волновая теория.

Прием, который встретили идеи де Бройля в научном мире, хорошо характеризуется следующим случаем, о котором рассказал Макс Борн. В 1925 г. Эйнштейн посоветовал Борну прочесть диссертацию де Бройля, сказав: «Прочтите ее! Хотя и кажется, что ее писал сумасшедший, написана она солидно».

4. КВАНТОВАЯ МЕХАНИКА

Принципы волновой механики были еще мало известны, когда была сделана другая, совершенно отличная попытка выйти из трудного положения, в котором оказалась теоретическая физика. Эта попытка была предпринята в 1925 г. очень молодым учеником Зоммерфельда Вернером Гейзенбергом (род. в 1901 г.) и получила быстрое развитие благодаря работам М. Борна и П. Йордана.

Гейзенберг проникся духом «копенгагенской школы», образовавшейся вокруг Бора, и посвятил свои первые работы применению принципа соответствия. Его теория родилась из сочетания этого принципа с новой феноменологической концепцией, которую он принял при изучении физических проблем. По мнению Гейзенберга, при построении физической теории нужно исключать все величины, которые недоступны нашему опыту, и пользоваться только теми, которые мы можем наблюдать. Например, в предшествовавших теориях атома фигурируют траектории, положения, скорости электронов, но кто же видел когда-нибудь траекторию электрона? Кто экспериментально определил хоть раз положение или скорость электрона? Мы знаем лишь стационарные состояния атома, переходы атома из одного состояния в другое, энергию, излученную или поглощенную при этих переходах. Любая теория атома должна принимать в расчет только эти величины. Удалось ли действительно Гейзенбергу осуществить эту свою философскую программу и исключить из теории все ненаблюдаемые величины - это уже другой вопрос. Фактом остается, однако, то, что это новое направление построения физической теории знаменует собой важный этап в развитии современной физики (Следует отметить, чтсГпринцип «наблюдаемости» Гейзенберга несет на себе явный отпечаток позитивизма. Дальнейшее развитие физики, в особенности теории вакуума частиц, показало несостоятельность этих философских установок. - Прим. ред).

Понятия, которые могут быть связаны с опытом, нельзя выразить из-за их квантовой дискретности через обычные непрерывные математические функции; нужно было найти какие-то новые формы выражения. В выборе этого нового формализма Гейзенберг руководствовался, возможно, принципом соответствия. Классическая теория выражает любую величину, связанную с квантовой системой, с помощью разложения в ряд Фурье. Квантовая же теория расчленяет эту величину на элементы, соответствующие различным переходам атома. Согласно принципу соответствия, оба эти метода должны асимптотически совпадать при очень большом числе квантов. Исходя из таких соображений, Гейзенберг пришел к поистине революционной идее: так сказать, раздробить каждую квантовую величину, представив ее в виде таблицы чисел, аналогичных применяемым в математике матрицам (бесконечным).

Приняв такое представление, нужно было найти правила вычисления этих новых величин, и Гейзенберг, применяя принцип соответствия, сумел показать, что эти правила совпадают с правилами действий над матрицами, найденными Эрмитом и известными в математике, но не получившими еще до сих пор никакого применения в физике. Эти правила не всегда совпадают с правилами обычной алгебры, в частности произведение матриц, вообще говоря, не обладает свойством коммутативности. Оно зависит от порядка сомножителей, т. е. произведение первой матрицы на вторую не равно произведению второй матрицы на первую. Это очень важный факт для квантовой механики, настолько важный, что Дирак кладет его в основу своего изложения квантовой механики. Согласно Дираку, переход от классической механики к квантовой получается при замене величин, представляемых в классической механике обычными числами, на величины, представляемые «квантовыми числами», произведение которых не коммутативно.

Затем, по-прежнему руководствуясь принципом соответствия, Гейзенберг вводит в свою схему постоянную Планка, причем вводит ее таким образом, что в явлениях макроскопических, в которых величина h относительно мала, произведение механических величин оказывается всегда не зависящим от порядка множителей, так что здесь мы снова возвращаемся к классической механике. Мы не имеем возможности следить дальше за развитием этой теории, не прибегая к помощи соответствующего математического аппарата, который в квантовой механике является чуть ли не самой сутью этой теории.

Строгость и точность предложенного математического метода и полученные с его помощью результаты (доказательство существования стационарных состояний с квантованными значениями энергии, расчет энергетических уровней линейного осциллятора, атома водорода и т. п.) привели в восторг молодых физиков. Но излишняя абстрактность теории, ставившая на место физических понятий математические символы, заставляла думать, что физика вступила на дурной путь, тех ученых, которые, как и Эйнштейн, считали, что «всякая физическая теория должна быть такой, чтобы ее, помимо всяких расчетов, можно было проиллюстрировать с помощью простейших образов, чтобы даже ребенок мог ее понять» (Цитируется по книге L. De Вrоglie, Nouvelles perspectives en microphysique, Paris, 1956, p. 236).

5. ВОЛНОВЫЕ УРАВНЕНИЯ

Стройность логического построения теории де Бройля, не говоря уже о наглядности представления о волне, связанной с частицей (к чему мы еще вернемся в дальнейшем), привлекла внимание швейцарского физика Эрвина Шредингера (1887-1961) - преподавателя из Цюриха. Большой заслугой Шредингера является то, что он первым в 1926 г. нашел в явном виде уравнение для волн волновой механики и построил на его основе строгий метод рассмотрения задач квантования.

Это уравнение, полученное преобразованием классических уравнений в представлении Гамильтона, обладает той особенностью, что не все его коэффициенты представляют собой вещественные числа; в него входят и мнимые числа. В классической же физике уравнения распространения волн содержат всегда лишь вещественные числа, а если иногда вещественные функции и заменяются мнимыми функциями (или, точнее, комплексными), то там речь идет всего лишь о способе расчета. Между тем в волновой функции Шредингера, обычно обозначаемой теперь буквой ψ, мнимые коэффициенты принципиально неустранимы и поэтому как бы свойственны самому явлению, которое они описывают. Другими словами, если в классической физике волны соответствуют колебаниям реально существующей среды (например, воздуха при звуковых волнах) или предполагаемой среды (эфира в случае распространения света), то волну в волновой механике нельзя рассматривать как физическую реальность, соответствующую колебаниям какой-то среды. Впрочем, этот вывод лишь подтверждает то, что де Бройль интуитивно угадал: такой волне, как волна, сопряженная с частицей, не несущей энергии и распространяющейся в многомерном пространстве, нельзя приписать физического существования; это «фиктивная волна», как ее назвал де Бройль, или «волна-призрак», как ее окрестил Эйнштейн характерным для него образным языком, проникнутым юмором.

Эрвин Шредингер

При составлении своего уравнения Шредингер, как мы уже говорили, исходил из классических уравнений и, следовательно, из ньютоновской механики. Это означает, что его уравнение не принимало в расчет релятивистских поправок для больших скоростей частиц, т. е. уравнение было справедливо лишь для частиц с достаточной малой скоростью. Этим объяснялись некоторые недостатки уравнения Шредингера. Делались попытки устранить их, внося в само уравнение необходимые релятивистские поправки, однако лишь в 1928 г. П. А. М. Дирак, подвергнув острой критике имевшиеся к тому времени релятивистские уравнения, указал на необходимость большего обобщения и выдвинул свою теорию - теорию очень большого физического значения, но еще более необычную и абстрактную по форме, чем волновая и квантовая механика. Одно из главных достоинств теории Дирака то, что из нее почти автоматически вытекает гипотеза о вращающемся электроне, которую Уленбек и Гаудсмит выдвинули в 1925 г. и которая наделала много шума. Согласно этой гипотезе, электрон подобен заряженному шарику, вращающемуся вокруг одного из своих диаметров. Таким образом, электрон обладает собственным механическим и магнитным моментом. Для обозначения собственного вращения электрона и его механического момента Уленбек и Гаудсмит использовали английское слово «спин» [от глагола to spin (англ.) - вращаться], которое теперь принято всеми физиками и которое можно было бы, пожалуй, перевести словом «волчок». Гипотеза спина полностью подтвердилась, и, казалось, именно этого не хватало предшествовавшим теориям атома.

Теория Дирака гармонически сочетает теорию относительности, кванты и спин, которые до этого казались понятиями, совершенно не зависящими друг от друга. Еще одно удивительное следствие, вытекающее из теории Дирака, заключалось в том, что электрон может находиться также в состояниях с отрицательной энергией, обладая свойствами, весьма странными для нашего физического мышления. Чтобы ускорить такие электроны, нужно отнять у них энергию, а чтобы привести их в состояние покоя, нужно придать им энергию!

Эти выводы вызвали живые споры между сторонниками и противниками теории. Дирак попытался объяснить столь странные выводы своей теории с помощью остроумной гипотезы, которая казалась, однако, слишком надуманной и приводила к заключению о возможности существования положительного электрона. Физики в большинстве своем отнеслись скептически к такому выводу, нов 1932 г. сначала Андерсон, а затем Блэккет и Оккиалини показали, что при ядерных распадах, вызываемых космическими лучами, появляются частицы, которые ведут себя именно как положительные электроны, предугаданные теорией Дирака. Впоследствии положительные электроны (или позитроны, как их стали называть) были получены искусственным путем при бомбардировке жесткими γ-лучами некоторых тяжелых элементов. Было определено отношение заряда частицы к массе, оказавшееся точно таким же, как и у отрицательных электронов. Сейчас, очевидно, уже нельзя сомневаться в существовании позитрона, который рассматривается теперь как одна из элементарных частиц.

6. ЭКВИВАЛЕНТНОСТЬ ВОЛНОВОЙ И КВАНТОВОЙ МЕХАНИКИ

С помощью своего уравнения Шредингер мог приступить к решению проблемы нахождения стационарных состояний квантовой системы и стационарных значений энергии. Таким образом, Шредингер определил энергетические уровни, а значит, и спектральные термы, получив во многих случаях те же значения, которые давала старая теория квантов. Во многих других случаях, однако, величины, полученные Шредингером, отличались от результатов старой теории квантов и при этом лучше соответствовали данным опыта. Самый простой случай - это случай с линейным осциллятором. Еще при самом зарождении квантовой теории Планк произвел квантование энергии линейного осциллятора, положив квантованные значения энергии целыми кратными кванта энергии hv. Но некоторые физические явления (например, полосатые спектры двухатомных молекул) лучше объяснялись4 при предположении, что квантование линейного осциллятора происходит по полуцелым кратным кванта энергии, т. е. энергия равна произведению кванта hν на последовательность чисел 1/2, 3/2, 5/2 ..., (2n+1)/2. Так вот, метод квантования по Шредингеру приводил именно к таким полуцелым кратным, существенно отличаясь здесь от старой теории квантов.

Квантовая механика Гейзенберга приводила к тем же результатам. Шредингер чувствовал, что здесь речь идет не о случайном совпадении, что за этим совпадением результатов кроется гораздо более глубокая причина - фактическая тождественность волновой и квантовой механики. Такой вывод, строго доказанный Шредингером в его знаменитой работе 1926 г., чрезвычайно поразил физиков того времени, так как понятия и математические методы обеих теорий очень сильно различались. И все же из доказательства Шредингера несомненно следовало, что квантовая механика представляет собой другую математическую формулировку волновой механики. Волновая механика более близка интуитивным представлениям физиков, требует менее сложных математических средств и поэтому чаще применяется, зато квантовая механика часто гораздо быстрее приводит к желаемым результатам.

7. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА

Выдвинутые волновой механикой необычные понятия, чтобы окончательно укрепиться, нуждались в опытной проверке. Еще в своем втором докладе Академии наук де Бройль говорил об экспериментальной проверке:

«Поток электронов, - писал он тогда, - проходя через очень тонкую щель, должен был бы дать явление дифракции. Именно таким путем, по-видимому, нужно будет искать опытное подтверждение наших идей» (L. De Вrоglie, Quanta de lumierc, diffraction et interference, Comptes rendus de l'Ас. Sc. de Paris, 177, 549 (1923)).

Речь идет, конечно, лишь о схеме. Можно легко подсчитать, что длина волны, связанной с движением электрона не очень большой скорости, равна, если не принимать во внимание релятивистскую поправку, самое большее нескольким ангстремам (А именно длина волны 1, связанная с движением электрона небольшой скорости, равна λ=12,24√V/•10^-8 см (V - в вольтах). Так как нужно применять электроны, ускоренные разностью потенциалов порядка десятков вольт, то достаточно провести простой арифметический подсчет, чтобы получить результат, указанный в тексте), т. е. порядка длины волны рентгеновских лучей. А мы уже видели, что линии искусственной дифракционной решетки, как бы близко они ни располагались, все же всегда, если не прибегать к методу Комптона, слишком далеки друг от друга, чтобы можно было на них наблюдать дифракцию рентгеновских лучей. Тем более нельзя было надеяться наблюдать дифракцию с помощью простой щели.

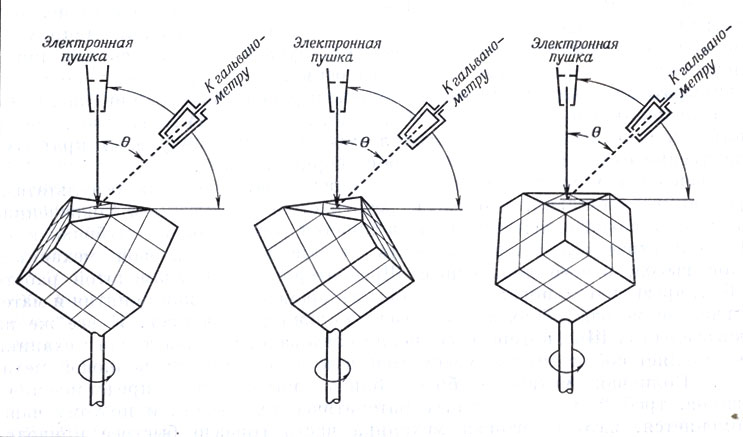
Схема опыта Дэвиссона и Джермера по дифракции электронов (С. J. Davissоn, The discovery of electron waves, Les Prix Nobel en 1937.) На плоскость кристалла никеля, показанного в виде куба со срезанным углом, направляется пучок электронов определенной скорости. Цилиндр Фарадея, служащий для сбора дифрагированных электронов, может перемещаться по дуге вокруг кристалла. Кристалл тоже может вращаться вокруг оси, совпадающей с направлением падающего пучка электронов. Таким способом можно измерять интенсивность дифрагировавших лучей в разных направлениях. Эти опыты дали подтверждение (в том числе и количественное) соотношения де Бройля. На рисунке изображены три различных положения кристалла

Еще за несколько лет до того, как де Бройль опубликовал статьи о волновой механике, К. Дж. Дэвиссон провел с сотрудниками лаборатории фирмы «Белл телефон» в Нью-Йорке экспериментальные исследования явления испускания вторичных электронов (т. е. электронов, выброшенных в результате столкновения с препятствием других электронов, называемых первичными) и получил довольно интересные, но трудно объяснимые теоретически результаты. Летом 1926 г. Дэвиссон обсуждал результаты своих опытов в Лондоне с Ричардсоном, Борном и Франком и пришел к выводу, что его исследования могли бы служить опытным подтверждением теории де Бройля. Возобновив с этой целью опыты, Дэвиссон и его сотрудник Л. Джермер уже следующей весной смогли объявить о замеченном ими явлении дифракции электронов. Пучок электронов падал перпендикулярно плоскости кристалла никеля; дифрагировавшие электроны собирались цилиндром Фарадея, перемещавшимся по дуге вокруг кристалла. Через несколько месяцев Джордж П. Томсон (Независимо от Томсона дифракция электронов была обнаружена советским физиком П. С. Тартаковским. - Прим. ред) вместе со своим учеником А. Ридом, вскоре погибшим в автомобильной катастрофе в возрасте всего лишь 22 лет, независимо от Дэвиссона обнаружил дифракцию электронов, направляя их на металлическую фольгу или на кристаллические порошки и применив метод фотографирования, что не только упрощало громоздкое приспособление Дэвиссона, но делало также доказательство дифракции электронов наглядным и допускало непосредственное сопоставление с картиной дифракции рентгеновских лучей. Дэвиссон так комментировал одновременность и независимость опытов, проведенных в Нью-Йорке и в маленьком городке Абердине:

«То, что поток электронов обладает свойствами волновых лучей, впервые было открыто в 1927 г. в большой промышленной лаборатории в центре огромного города и в лаборатории маленького университета на берегу холодного и пустынного моря. Это совпадение тем более покажется удивительным, если мы вспомним, что средства, необходимые для этого открытия, имелись в любой лаборатории мира и постоянно употреблялись там уже более четверти века. И все же в этом совпадении не было ничего исключительного. Открытия в физике делаются тогда, когда приходит их время, и не раньше. Наступает момент, и неизбежное совершается чуть ли не в одно и то же мгновение даже в самых удаленных друг от друга местах» (С. J. Davissоn, The discovery of electron waves, Nobel lecture, Les Prix Nobel en 1937, Stockholm, 1938).

Проще можно было бы сказать, что лаборатории уже в течение 25 лет располагали всеми инструментами, необходимыми для открытия дифракции электронов, но что еще не было волновой механики, которая могла бы подсказать эти исследования.

Экспериментальная проверка продолжалась с помощью различных приборов и в различных условиях, и, наконец, в 1929 г. Руппу удалось осуществить дифракцию электронов с помощью простой оптической решетки при почти скользящем падении в соответствии со способом, указанным еще Комптоном. Как это часто случается, экспериментальная проверка дифракции электронов, потребовавшая столько изобретательности и усилии первых экспериментаторов, сейчас в результате усовершенствования технических средств представляется нам такой простой, что может быть проведена даже на лекции как демонстрационный опыт.

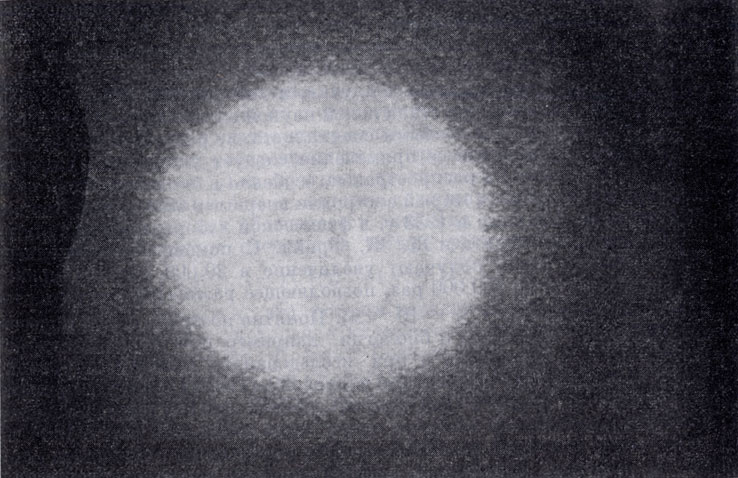
Первая фотография дифракции электронов, которую получили Дж. П. Томсон и А. Рид, направляя электроны на тонкую целлулоидную пленку. (Nature, 1927.) Световое пятно в центре окружено кольцами, напоминающими гало вокруг Солнца

Дифракцию испытывают и атомарные пучки (как это показали впервые в 1929 г. Штерн и Эстерман в опытах с атомами водорода), молекулярные пучки, одним словом - любые корпускулярные лучи. Опыты, проводившиеся при самых различных скоростях, подтвердили точность основных соотношений, связывающих волну и частицу. При больших скоростях экспериментальные данные совпадают с расчетными при учете релятивистских поправок, так что эти опыты являются косвенным доказательством справедливости теории относительности.

Явление дифракции электронов сразу же было применено для исследов ния поверхностных явлений и структуры малых кристаллов.

Благодаря меньшей проникающей способности электронов они оказались гораздо более подходящими, нежели рентгеновские лучи, для изучения тонких пленок вещества. В частности, этот метод получил промышленное применение при изучении смазочных свойств различных масел и свойств поверхностных слоев различных металлов. Перечислить все случаи, в которых применяется дифракция электронов, нелегко, она стала целой наукой со своими собственными методами, особой техникой и особыми специалистами, работающими в этой области. Но один из примеров ее применения следует упомянуть, так как он широко известен и весьма распространен, особенно в биологии. Речь идет об электронном микроскопе, который построили впервые в 1931 г. фон Боррис и Руска, а затем во Франции в 1933 г. в физической лаборатории факультета наук в Безансоне Р. Фритц и Ж. Ж. Трийя. С помощью электронных микроскопов обычно легко получают увеличение в 20 000 раз, но можно получить увеличение и до 100 000 раз, позволяющее различить две точки на расстоянии примерно 30 А(1А=10^-8 см). Понятно поэтому, сколь полезен этот инструмент для медицины и биологии, например при изучении морфологии бактерий, ультравирусов и при исследованиях раковых опухолей.

Первый крупный успех применения волновой механики к ядерной физике относится к 1928 г., когда Гамов дал объяснение прохождению α-чаетиц через потенциальный барьер тяжелых ядер. Через несколько лет, в 1934 г., Ферми с помощью волновой механики удалось очень просто объяснить одно открытое им явление, казавшееся парадоксальным: медленные нейтроны (т. е. имеющие скорость порядка скорости теплового движения) особенно эффективно вызывают искусственную радиоактивность, если ими бомбардировать ядра. Но об этом и о других применениях волновой механики мы будем еще говорить более подробно в следующей главе.

Раз волновая механика получила такое широкое применение в ядерной физике, легко понять, что она должна была также найти успешное применение и в теоретической химии для описания и предсказания целого ряда химических реакций, а главное - для объяснения сущности химической валентности, остававшейся до сих пор тайной.

Наконец, волновая механика привела к пересмотру всех теорий строения вещества. Сейчас без нее нельзя понять также и целый ряд макроскопических явлений; она стала наукой, необходимой не только физикам, химикам и биологам, но и инженерам.

Если считать, что ценность той или иной теории измеряется количеством и значительностью ее практических применений, то вопреки общему мнению следовало бы сказать, что волновая механика - одна из самых плодотворных теорий современной физики.

8. КВАНТОВАЯ СТАТИСТИКА

Представляя фотон как частицу, физики, естественно, попытались получить законы излучения, рассматривая пространство, занятое излучением, как занятое «фотонным газом». К этому газу они применяли те же статистические критерии (с соответствующими изменениями), которые классическая физика применяла с таким успехом к обычным газам для определения распределения скоростей, а следовательно, и энергии между n молекулами газа с общей энергией Е, содержащимися в объеме V. Однако фотонный газ существенно отличается от обычного газа, состоящего из молекул, тем, что в последнем число частиц постоянно, тогда как в фотонном газе оно переменно, так как стенки объема могут поглощать или испускать излучение, т. е. фотоны. Другое различие вытекало из квантовой гипотезы, которая уменьшала число возможных состояний рассматриваемой фотонной системы. С учетом этих двух различий задача ставилась в соответствии с представлениями классической физики в применении к фотонному газу, заполняющему некую полость в черном теле. При этом получался закон излучения Вина, который, как мы видели в гл. 13, противоречит опыту.

В 1924 г. индийский физик Д. М. Бозе преодолел это противоречие, предположив, что к фотонам нельзя применять законы статистики обычных материальных частиц, которые до сих пор казались физикам не только единственно допустимыми, но и единственно мыслимыми. Речь идет в сущности вот о чем. Всякая статистическая проблема сводится в общем к определению того, как может распределиться определенное число объектов в определенном числе ячеек. Для простоты предположим, что у нас два объекта, обозначенные знаками + и -, которые должны разместиться в двух ячейках, причем каждая из них обозначается скобками ( ). Согласно классической статистике, возможны следующие четыре распределения:

( + )(-); (-)( + ); (+ -)( ); ( )(+ -).

Но Бозе, учитывая, что фотоны неразличимы между собой, отрицал их индивидуальность, которая в классическом понимании отнюдь не то же самое, что различимость. Поэтому Бозе принял, что первые два распределения - это одно и то же, так что распределение двух фотонов (обозначаемых теперь одним и тем же знаком +) в двух ячейках может произойти одним из трех способов:

( + )( + ); (+ +)( ); ( )(+ +).

Независимо от того, удовлетворительно или нет объяснение Бозе, остается фактом, что, внося в классическое статистическое рассмотрение предложенную им поправку, мы приходим к закону Планка, который, как мы знаем, целиком подтверждается опытом.

Эйнштейн редактировал немецкий перевод статьи Бозе. Одновременно он получил от Ланжевена рукопись докторской диссертации Л. деБройля, в которой тот выводит закон Планка из своей волновой гипотезы. Л. де Бройль заметил, что поскольку с движением частицы связывается распространение волны, то следует принимать во внимание только стационарные волны, соответствующие резонансу в данном объеме, в связи с чем он изменил статистический расчет классической механики. Эйнштейна живо заинтересовали эти результаты де Бройля; он сопоставил их с результатами Бозе в двух своих статьях 1924 и 1925 гг., в которых Эйнштейн применяет новые статистические законы и к обычным газам. В результате была создана интересная теория, объясняющая поведение газов в обычных условиях при не очень низких температурах.

Успех этой новой статистики, названной статистикой Бозе - Эйнштейна, побудил физиков рассмотреть вопрос о том, не будет ли целесообразно и в других случаях видоизменить критерии классической статистики.

В 1926 г. Энрико Ферми (1901-1954) заметил, что, даже для идеального газа если потребовать выполнения принципа Нернста, то необходимо считать величину удельной теплоемкости при постоянном объеме, даваемую классической термодинамикой для одноатомного газа, лишь приближенным значением, пригодным для высоких температур, но что в действительности эта удельная теплоемкость должна стремиться к нулю по мере приближения температуры к абсолютному нулю. Для объяснения изменения удельной темплоемкости с температурой, нужно, чтобы движение совершенного газа было квантовано. Этой проблеме квантования Ферми посвятил важную статью, появившуюся в том же году в Трудах Академии деи Линчей. Правила квантования, данные Зоммерфельдом, представлялись Ферми недостаточными, потому что, хотя они и приводили к выражению для удельной теплоемкости, стремящейся к нулю по мере приближения к нулю абсолютной температуры, эта теплоемкость, однако, оказывалась зависящей от общего количества газа вопреки всем данным опыта. Поэтому в правила Зоммерфельда нужно было ввести поправки, учитывая, что у совершенных газов, согласно Ферми, частицы, неразличимы между собой. Опираясь на принцип Паули, Ферми сформулировал свою основную гипотезу:

«Предположим, что в нашем газе определенным набором квантовых чисел может характеризоваться не более одной молекулы, и покажем, что эта гипотеза приводит к последовательной теории квантования совершенного газа и что она, в частности, объясняет предсказанное уменьшение удельной теплоемкости при низкой температуре и дает, точное значение для константы в выражении для энтропии совершенного газа» (Enrico Fermi, Sulla quantizzazione del gas perfetto monoatomico, Rend. Acс. Lincei, classe sc. fis. mat. e nat./(6), 3, 147 (1926). ).

Эта гипотеза была равносильна принятию для этого газа, подчиняющегося принципу запрета Паули, нового статистического критерия, предложенного почти одновременно и независимо от Ферми П. А. М. Дираком. Этот критерий, если снова прибегнуть к тому простейшему примеру, который мы уже приводили, состоит в предположении, что две частицы могут разместиться в двух ячейках только одним-единственным способом, а именно (+) (+). Обе новые статистики и соответствующие им термодинамические теории, сильно отличающиеся друг от друга, асимптотически переходят в классическую статистику, когда квантовая дискретность становится все менее существенной. В применении к реальным газам различия между этими двумя квантовыми термодинамиками и классической термодинамикой так незначительны, что их невозможно обнаружить. Поэтому новые статистики нельзя было экспериментально проверить по данным о реальных газах. Статистика Бозе - Эйнштейна была экспериментально подтверждена данными об излучении черного тела, а статистика Ферми - Дирака - электронной теорией металлов, как показал Зоммерфельд.

Теперь уже считается установленным в физике, что все частицы атомарных масштабов делятся на две категории: одни частицы, подчиняющиеся принципу запрета Паули, как, например, электроны, протоны и некоторые атомные ядра, следуют статистике Ферми - Дирака и называются по предложению Дирака фермионами; другие частицы, не подчиняющиеся принципу запрета, как, например, α-частицы, фотоны и некоторые атомные ядра, следуют статистике Бозе - Эйнштейна; их Дирак предложил называть бозонами.