Теория ферм в трудах русских ученых

Конструкции ферм, как мы видели, являлись объектами, на которых велись разработки методов и приемов расчетов сооружений. На фермах иллюстрировались идеи взаимных перемещений, идеи взаимности работ, идеи минимума потенциальной энергии и т. п. Одновременно создавалась теория ферм.

Научное понятие "ферма" впервые было дано Максвеллом в 1864 г. Он определил, что ферма есть система линий, соединяющих известное количество точек. Жесткой фермой называется система, в которой расстояние между какими-либо точками не может быть изменено без изменения длины одной или нескольких линий, соединяющих эти точки. О роли раскосов в фермах писал перед этим У. Д. Ранкин.

Развитием плоских ферм занимались русские инженеры Ф. С. Ясинский и В. Г. Шухов. В 1894 г. Ф. С. Ясинский начал читать курс статики сооружений в Петербургском институте инженеров путей сообщения. В этом курсе статика сооружений была обобщенным изложением строительной теории [74]. Ф. С. Ясинский исследовал аналитические и графические способы расчета ферм и внес в эти расчеты свой способ "сомкнутых сечений", чем обобщался способ "вырезания узлов". Известный в то время прием расчета ферм Геннеберга Ф. С. Ясинский обобщил методом "замены связей". Рассматривая пространственные конструкции, Ф. С. Ясинский предложил применять такие системы, опоры которых допускают сохранение подобия сечения и при воздействии температуры позволяют сооружению занять положение, подобное первоначальному.

В 90-х годах XIX в. В. Г. Шухов исследовал фермы для перекрытия зданий. Он исходил из того, что аналитические и графические методы расчета ферм не дают ответа на вопрос о целесообразности и экономической выгодности рассчитываемой конструкции. Стремясь строить не только прочно, но и экономически целесообразно, В. Г. Шухов применил критерий наименьшего расхода материала для ферм. В труде "Стропила" (75) он дал аналитический расчет ферм, позволяющий определять усилия в элементах ферм, веса этих элементов и наивыгоднейшее геометрическое расположение всех частей ферм, при котором вес употребленного материала будет наименьшим. Раскрыв сущность напряженного состояния стропильной фермы, Шухов показал, что при равномерно распределенной нагрузке та ферма будет наиболее выгодной и на нее пойдет меньше материала, для которой изгибающий момент будет равен нулю, и что ферма, имеющая параболическую форму верхнего пояса, отвечает поставленной задаче.

При односторонней равномерной нагрузке в верхнем поясе параболической фермы имеется изгибающий момент, но он в 2 раза меньше, чем в ферме с прямолинейным верхним поясом. Исследовав характер сжатия верхних поясов в фермах двух этих типов, В. Г. Шухов показал, что ферма, испытывающая наименьшее напряжение материала, должна при равномерной нагрузке иметь форму параболы. Он тщательно проанализировал расположение решеток в фермах и вывел формулы для определения формы стропильных ферм с точки зрения их наивыгоднейшего веса.

83. Остекленное перекрытие здания Верхних торговых рядов (ныне ГУМ) в Москве

На основе глубокого и тонкого анализа арочных параболических ферм В. Г. Шухов пришел к выводу, что раскосы в фермах этого типа можно заменить хордами, связывающими точки параболического пояса фермы с ее опорами. Это облегчает решетку фермы и упрощает ее конструкцию. В. Г. Шухов получил легкие конструкции арочных стропил с тягами. Эти конструкции можно увидеть в остекленных перекрытиях ГУМа на Красной площади (рис. 83) и Петровского пассажа в Москве. Шуховым созданы металлические конструкции Брянского (ныне Киевский) вокзала (рис. 84).

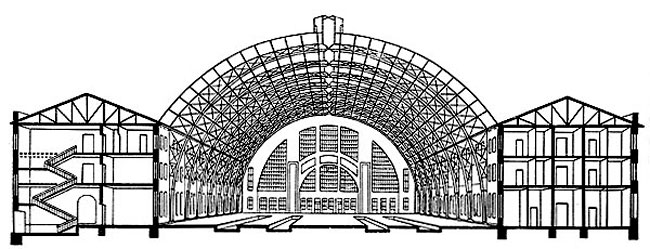
84. Разрез Брянского (ныне Киевский) вокзала в Москве

Вес арочных ферм зависит от шага ферм в перекрытии здания, от длины панелей арки между тягами и от шага обрешетки для кровли. Эту зависимость В. Г. Шухов выразил математически и пришел к выводу, что, во-первых, вес материала, сопротивляющегося действию изгибающих моментов в покрытии, отнесенный к единице площади перекрытия, уменьшается с уменьшением длины панели и расстояния между фермами и, во-вторых, минимум этого веса получается тогда, когда обрешетки нет, а расстояние между фермами равно расстоянию между обрешетками, причем ферма разбита на панели длиной, равной шагу обрешетки.

При обычных типах ферм получить эти наилучшие условия невозможно, так как от уменьшения шага ферм растет расход материала на единицу перекрываемой площади, а от уменьшения панелей в фермах увеличивается число раскосов в них и число связей между фермами.

В. Г. Шухов нашел исключительно правильный и научно обоснованный выход из создавшегося противоречия. Он писал, что единственный практически возможный путь для уменьшения размеров (длины панелей и расстояния между фермами) в покрытиях заключается в применении устройства сетчатых поверхностей.

Таким образом, русские ученые Ф. С. Ясинский и В. Г. Шухов создали теорию стропильных ферм, обосновав условия образования их поясов, раскосов, стоек и опорных конструкций. Кроме того, В. Г. Шухов указал условия перехода от одного качественного состояния стропильных перекрытий к другому, более высокому по форме и внутреннему содержанию - к сеточным покрытиям. В. Г. Шухов с большим успехом строил такие покрытия на рубеже XIX и XX столетий.