Нужны ли головоломки?

Вы любите головоломки? И конечно, не откажетесь решать их, если бы вас попросили это делать, так сказать, для пользы науки. Вот почему у психолога Якова Александровича Пономарева, который предлагал решать головоломки буквально всем встречным, не было нехватки в желающих. Принять участие в таких веселых опытах хотелось каждому. Тем более что тут не надо было ничего изобретать ни всерьез, ни понарошку. Отгадывай себе головоломки - и все. Работа несложная и даже занятная.

На деле все оказалось еще проще. Любителям веселого досуга предлагалось решить одну и ту же задачку, которая условно называлась: "Четыре точки". Через четыре точки (как бы вершины квадрата) надо было провести три прямые линии; не отрывая карандаша. Давалось на это десять минут.

"Да куда нам столько? - удивлялись участники опыта. - И двух минут хватит". И брались за карандаш и бумагу. Но проходили положенные десять минут, потом еще десять, а они все продолжали чертить зигзаги в бесплодных попытках очередным росчерком найти решение.

Вот как это выглядело:

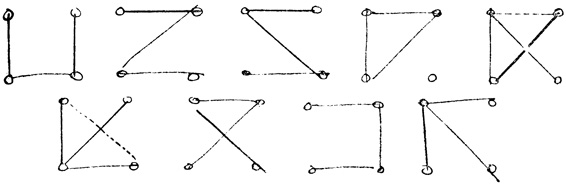
Головоломка

И почему-то почти никто не догадался сразу, что до просто вписать квадрат в треугольник, иными словами выйти за пределы заданной фигуры, а не мыкаться внутри нее. А ведь нельзя сказать, что решение уж очень сложно. Надо было лишь подойти к задаче творчески - догадаться, что условие не ограничено контурами квадрата. Самое удивительное, что такого рода ограничение участники опыта мысленно создали сами: никто ни слова не говорил им, что нельзя продолжить линии за пределы квадрата - сработала привычка мыслить по шаблону, только данными категориями.

Надо сказать, что столь распространенная косность мышления оказалась неожиданной и для ученых. 600 человек из побывавших в лаборатории Пономарева не смогли самостоятельно решить задачу о четырех точках, хотя старательно ломали над ней голову. Вырваться за пределы огороженного четырьмя точками участка оказалось для них непреодолимой трудностью - они упорно толклись внутри квадрата.

Сотни людей признали задачу нерешаемой, а решить ее было так легко. Может быть, сказывается отсутствие навыка? Пономарев стал готовить участников опыта заранее. Он объяснял им правила игры в хальму, где используется шахматная доска. По ходу игры участники будущего опыта должны были перескочить на шахматной доске одним ходом белой фишки через три черных и снова вернуться на свое место. Иными словами, они как раз описывали треугольник около квадрата, вернее пресловутых четырех точек.

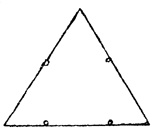
Разгадка совсем рядом

После этого прямо на шахматную доску накладывалась прозрачная калька с четырьмя точками, расположенными как раз на месте участвовавших в игре фишек. Оставалось повторить маршрут, по которому только что двигалась рука, но и на этот раз участники опыта продолжали ломать голову над уже фактически найденным решением.

Подсказка не помогла: участники опыта не видели никакой связи между шахматным этюдом и головоломкой о четырех точках.

Тогда психологи изменили тактику. Они давали студентам возможность вдоволь поломать голову над задачей, а потом предлагали поиграть в хальму. На этот раз подсказка попала в цель: примерно половина добровольных мучеников науки моментально решили головоломку. Остальным не помогла даже своевременная подсказка.

Любопытно, что большинство решивших задачу по подсказке даже не сознавало, откуда к ним пришло решение. Они уверяли, что догадались вдруг, случайно, как бы по наитию и т. п. Они так мысленно и не соединили свои ходы на шахматной доске и чертежи на бумаге. (Не так ли и ученые или изобретатели нередко не замечают подсказки, которую им подбрасывает жизнь?)

Другие, напротив, подошли к подсказке сознательно, сразу увидев нужную схему решения, подобно тем изобретателям, которым помог "случайный" взгляд на крышку кипящего чайника или падающее яблоко.

Психолога Пономарева чрезвычайно заинтересовали все перипетии решения злополучной задачи с четырьмя точками. Он, что называется, "заболел" этим на всю жизнь. Все усложнял и усложнял он свои опыты, увеличивая количество точек, меняя время подсказок и форму эксперимента.

Теперь уже речь шла о шестнадцати, двадцати четырех или тридцати двух точках. Вместо карандаша и бумаги он соорудил доску со штырями, на которую можно было вешать специальные планки. Все варианты проб тщательно анализировались.

И они подтвердили неэффективность подсказок, выданных заранее. Подсказки же, данные после неудачных проб, безотказно действовали лишь на определенном этапе, когда интерес к поискам решения еще не утратился и вера в то, что задача будет решена, не угасла. Слишком ранняя подсказка тоже проскакивала впустую.

Выходит, надо было основательно поломать голову самому, чтобы сознательно или бессознательно оценить подсказку, - иными словами, суметь поймать случай, который вознаграждает тех, кто его заслуживает. В итоге Пономарев написал целую книгу. Он так назвал ее "Психология творческого мышления", хоть она, по его собственному признанию, не исчерпывает всех проблем творчества, а посвящена лишь изучению того, как люди решают задачи-головоломки, значение книги гораздо шире.

Дело в том, что исследование наших мыслительных ходов при решении головоломок стало одним из основных способов изучения творческого мышления. Почему психологи отдали в данном случае предпочтение не обычным задачам, а своего рода загадкам? Да прежде всего потому, что собственно мышление, как мы уже говорили, начинается там, где есть проблема, иначе говоря, такая ситуация, в которой не все известно, что-то не раскрыто, неопределенно, вызывает вопросы. Но если в обычной задаче ответ на возникшие вопросы надо искать чисто логическим путем, рассуждая и делая определенные выводы, то задачу-головоломку не решить простым доказательством.

Тут нужно не только проанализировать проблему, выяснить, что дано, что неизвестно, и найти искомое, а прежде еще и распутать специально запутанные условия задачи. Ведь головоломка характерна как раз тем, что при формулировке задачи нарочно подчеркнуты несущественные для ее решения обстоятельства, тем самым важные стороны проблемы оказываются заслоненными, замаскированными и нередко направляют мысль по ложному пути.

Задачка

Вот одна из таких задач - наиболее простая: из точки А в восточном направлении до точки В самолет долетел за 80 минут, а из точки В в западном направлении до точки А - за 1 час 20 минут. Почему?

Или еще, посложнее: два велосипедиста едут навстречу друг другу со скоростью 15 километров в час. Когда они находятся на расстоянии 30 километров друг от друга, с руля одного из них слетает муха и со скоростью 20 километров в час летит к встречному велосипедисту. Достигнув его, она поворачивает обратно к первому велосипедисту. Долетев до него, снова поворачивает назад и т. д. Сколько километров пролетит муха?

В первом случае уводящим в сторону условием служит указание на западное и восточное направление полета. Оно невольно заставляет думать о скорости вращения Земли, которое для решения задачи никакого значения не имеет. Важно здесь другое: догадаться, что 80 минут и 1 час 20 минут - одно и то же, а стало быть, и решать нечего. Самолет как от до В, так и от В до А пролетает за одинаковое время.

В истории с мухой и велосипедистами тоже ответ ан в самих условиях задачи, только он замаскирован. Нет необходимости считать количество мушиных перелетов, как это хочется поначалу, они к делу не относятся. Ведь скорость мухи нам дана: 20 километров в час. А летать она будет ровно час. Так как расстояние между велосипедистами равно 30 километрам и пройдут они до встречи каждый по 15 километров со скоростью, как сказано, 15 километров в час. Иными словами, им понадобится один час, чтобы встретиться, а именно это время отведено мухе на перелеты. Стало быть, муха при своей скорости преодолеет за этот самый час 20 километров.

Опять-таки нужно было догадаться, что надо не считать количество перелетов, а, сопоставив известные скорости и расстояния, сообразить, какова длина мушиного пути.

Зачем прибегать к такой маскировке истинных условий? Как раз для того, чтобы вы имели возможность поломать голову. Составители головоломок заставляют вас не просто логически рассуждать, а разгадывать хитрости. Они втягивают вас в своеобразную игру мысли, провоцируя на обходные пути, на поиски нестандартных решений, короче: заставляют проявляться скрытые творческие силы ума, чтобы меть возможность детально изучить их.

Вот почему головоломки очень близки к настоящим творческим задачам. Как в тех, так и в других существенные условия, ведущие к решению, как бы завуалированы второстепенными обстоятельствами. И надо суметь демаскировать главное, не направить мысль по ложному следу. Разумеется, в подлинных творческих задачах никто нарочно не путал условий, их маскировала или недосказала сама жизнь.

Если в условиях задачи просто не хватает каких-то звеньев, деталей - их надо искать. Но бывает и так, что вроде все дано, а наблюдаемая ситуация остается какое-то время непонятной нам, пока вдруг не наступает прояснение и все становится на свои места. Задача понимания тут сводится не к открытию действительно неизвестного, а к открытию свойств предметов, так сказать, закрытых для нашего ума. Это и есть замечательная способность видеть вещи в новом свете, иметь нестандартный угол зрения, без чего невозможно никакое творчество.

Итак, успех решения обычной задачи - в строго последовательном, доказательном рассуждении. А головоломки - в разгадке ее. Чтобы понять, в чем состоит механизм самой догадки, и проводил Пономарев свои бесконечные опыты.

Он рассматривал задачу с четырьмя точками и тремя прямыми. А его последователи использовали другие варианты головоломок, скажем, такой: из шести спичек сложить четыре равносторонних треугольника, сторона которых должна быть равна длине спички. Провокация здесь заключается в том, что спички даны на плоскости, а решить задачу можно только, построив объемную фигуру. Надо опять-таки догадаться выйти в третье измерение.

Давайте рассмотрим подробнее, как приходит эта догадка, для чего познакомимся с протоколом одного из подобных опытов. Участница думает вслух:

"Вспоминаю различные геометрические фигуры, так как не сталкивалась с ними давно. В школе я любила геометрию, а сейчас никак не могу вспомнить подходящей фигуры. Нет, просто так выкладывать не могу, я должна сначала подумать, представить себе".

Пробует чертить, рассматривая зарисованные фигуры, замечает: "Все время одной линии не хватает".

Затем опять пробует, говоря: "Смотрю, что получится. На два треугольника идет пять спичек. Есть шесть спичек. Для четырех самостоятельных треугольников нужно двенадцать спичек, значит, надо строить фигуру, так как в ней некоторые стороны будут общими. Можно легко построить из девяти спичек, тогда три общие. Но у нас шесть спичек, выходит, что каждая должна быть общей.

Если рассуждать чисто спекулятивно, то все стороны должны быть внутренними. Но ведь нет же такой фигуры, где все стороны были бы внутренними. Сторона - компонент фигуры. Линия ее ограничивает. Линия как-то связана с точками. Нет, это не расстояния между двумя точками, а след движущейся. Но это нам ничего не дает. Линия состоит из точек. Если взять круг, там все точки удалены от центра. А на линии? На линии все они находятся на одной поверхности. Нет, это нам ничего не дает, не то. Еще что-нибудь вспомнить. Линии, линии... Точки... Если пересечь две линии, то получим одну точку, но нам-то нужна не точка, нам нужна линия. А! Так линию можно получить при пересечении двух плоскостей. Ну да. Две плоскости, пересекаясь, образуют линию, понятно. Значит, в пространстве надо было строить, а я почему-то в плоскости пыталась".

Строит тетраэдр.

Создается впечатление, что мышление происходит так: сначала неудачные пробы, затем догадка ("ага-решение", как ее называют), после чего как бы новый - правильный - этап мышления. В действительности догадка не вклинивается в ход мышления извне, хотя и наступает как будто неожиданно. Она совершенно необходимый этап и служит как раз для демаскировки истинных условий задачи - в данном случае для преодоления ложной предпосылки о том, что решение должно быть на плоскости.

Больше того, догадка и есть творческий момент в мышлении. И несколько упрощая, можно сказать, что творческое мышление - это именно решение задач-головоломок: движение мысли от условий к требованиям и от вновь открывшихся требований к новым условиям. Ведь решить головоломку - значит распутать клубок причин и следствий.

Если речь идет о разгадке обычных головоломок, то это просто игра умственных сил, тренировка мозга в применении правил думания, своего рода умственная гимнастика. Если же о решении подлинно творческих, важных задач, тогда мы вправе говорить об исследовательском мышлении, проникающем в неизведанное, обнаруживающем скрытые свойства вещей. Так что если хотите стать первооткрывателями, тренируйтесь, ломайте голову над забавными задачками.