Топология кенигсбергских мостов

Оценив общий подход к соотношению науки и игры, посмотрим конкретно на вопрос. Тема интересует нас под одним углом зрения: ведь для науки игра не самоцель, ученый включается в нее не ради самой игры, а чтобы решать познавательные задачи. Тут и обнаруживается, что исследовательская работа сродни разгадыванию "китайских головоломок" (Д. Томсон), похожа на решение кроссвордов (Л. де Бройль), шарад, на поиски выхода из лабиринта и тому подобное.

Но как головоломки, кроссворды и чайнворды кем-то составляются, так и многочисленные загадки составлены природой и поставлены перед ученым. Заполняя строчки кроссворда, отгадчик, понятно, волен делать выбор любого слова, но подойдет-то лишь одно, которое и надо отыскать. Не таким ли образом складываются дела в научном поиске? Имея перед собой "пустые клетки" на карте знания, исследователь отыскивает необходимую информацию, чтобы заполнить ею эти клетки и воспроизвести целостную картину реальности. У него тоже есть выбор, но он ограничен вариантами, которые подготовила природа.

Игра увлекает перспективой, заставляя проявить творческие силы, и несет эвристическую функцию, помогая отысканию истины. Вначале рассмотрим те случаи, когда ученый не ставил целью решать научные задачи, а просто включался в игру. Но, играя, находил нечто ценное для науки.

Еще на рубеже первого и второго веков до нашего летоисчисления жил в Древней Греции (теперь мы бы назвали его изобретателем) Герон Александрийский. Дошли слухи, что он придумал немало занятных вещей: пожарный насос, сифон, водяной орган, теодолит и много других изделий.

Особенно удивительным было устройство эолипил, своеобразная паросиловая установка (Эол - у древних греков бог ветров). Пар, вырываясь из трубочек, приводил в движение стеклянный шар. В сооружении Герона видят прообраз паровых турбин. А иные считают даже, что эолипил представляет, по существу, первый, пусть примитивный, зародыш реактивного двигателя (стоит лишь подвести под это экспериментальное чудо теоретическую базу). Во всяком случае, появившееся тысячелетия спустя, в середине XVIII века, так называемое "Сегнерово колесо" (дитя венгра Сегнера) демонстрируется в курсах физики как прибор, работающий на принципах реактивного механизма. У Сегнера колесо, не имеющее обода, приводится в движение водой. Вытекая из трубок, заменяющих спицы, вода и производит отталкивающую силу.

Мы не знаем и не узнаем ход мыслей Герона. Едва ли он рассчитывал на промышленное внедрение своего эолипила. Знаем только, что его изобретение использовалось как игрушка, развлекавшая тогдашнюю элиту. Это нам и нужно для нашей темы. Приступая к сооружению подобных вещей, Герон как бы задавал игровую ситуацию, то есть не ставил заведомо практических, тем более научных целей, а действовал просто из любопытства, что получится.

Поучителен и другой факт. Однажды Л. Эйлер заинтересовался чисто игровой задачей о кенигсбергских мостах.

Река Мемель, протекающая в районе Кенигсберга (ныне Калининград), разделяется в устье на два рукава, которые то сходятся в один поток, то расходятся. Город соединен мостами. Получилась целая сеть из семи мостов. Задача формулировалась так: надо последовательно обойти все семь мостов, но при этом ни разу не возвратиться назад, то есть не проходить какой-либо отрезок пути дважды.

Рассказывают, что Л. Эйлер эту задачку решал в часы отдыха, то есть принимал ее как игру, напоминающую поиск выхода из лабиринта. Впоследствии обнаружилось, однако, что эта была одна из первых задач с топологическим содержанием, учитывающим свойство непрерывности пространства.

Так зарождались идеи новой науки - топологии, получившей основательное развитие в середине прошлого столетия в трудах англичанина А. Кэли и немцев И. Листинга и А. Мёбиуса. Она изучает свойства фигур, не изменяющиеся при любых деформациях, производимых без разрыва и склеивания. Задача о путешествии через кенигсбергские мосты как раз и предлагала найти "безразрывный" (топологически выверенный) маршрут.

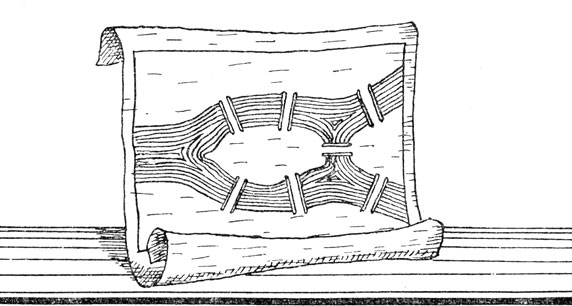
Топология кенигсбергских мостов

Что здесь отгадчика ждала действительно увлекательная игра, читатель может убедиться сам, попробовав решить эту задачу с простым условием. Стоит лишь попытаться, и вы окажетесь в плену этого забавного времяпрепровождения.

Игровая ситуация продиктовала еще одну топологическую задачу, решение которой также подвинуло разработку топологических свойств.

Речь касается известной теоремы о четырех красках, доказанной лишь совсем недавно. Практика нанесения географических карт показывала, что для получения любой из них достаточно иметь четыре краски, чтобы нигде на карте два соседних района не имели одинакового цвета.

Долгое время это считалось само собой разумеющимся, и никаких проблем не возникало. Но вот возник вопрос: а почему, собственно, достаточно именно четырех цветов? Так появилось "дело" о четырех красках.

Известно, что, если где-то закрадывается неясность, ученые такое положение не могут оставить без внимания. Однако усилия многих из них оказывались безрезультатными при решении такой, казалось бы, легкой задачи с "головоломным" оттенком: она перерастала в научную проблему.

...Однажды знаменитый немецкий математик конца прошлого - начала нынешнего столетия Г. Минковский, работающий в Гетингене, придя на лекцию по топологии, заявил: "Эта теорема не была до сих пор доказана лишь потому, что ею занимались математики третьего сорта. Я уверен, что мне удастся ее доказать". Заявил и, не откладывая в долгий ящик, тут же приступил к делу. Время шло, вот и лекция на исходе, однако доказательство не получалось. Минковский, все еще не теряя оптимизма, отложил решение до следующей лекции. Увы! В следующий раз произошло то же самое.

Так продолжалось несколько недель. И вот одним пасмурным утром, сопровождаемым раскатами грома, он вышел к слушателям и объявил: "Небеса разгневаны моим высокомерием. Мое доказательство о четырех красках также неверно". И стал продолжать лекцию с того места, где остановился несколько недель назад, когда пообещал расправиться с задачей о красках.

Лишь в середине 70-х годов нашего века, то есть долгие десятилетия спустя, американские математики К. Ап-пель и В. Хакен доказали, что любую карту можно раскрасить правильным образом, используя всего четыре цвета, подтвердив тем самым правомерность действий составителей географических карт. Но ответ был найден с помощью компьютера (вот уж кто работал, определенно опираясь на правила игры).

Эта история примечательна. Ведь саму по себе задачу о красках едва ли назовешь научной, обыкновенная, сугубо практическая задача, каких в жизни немало (лишь единицы вырастают из них до уровня научных). Тем не менее решение удалось только на основе научных методов и, надо полагать, в какой-то мере, пусть и не крупно, продвинуло науку вперед.

Здесь не крупно, а вот в других случаях находим значительное продвижение. Мы имеем в виду создание теории вероятностей. Это еще одна страница взаимоотношений науки и игры.

Увлечение ими началось в регионах античности и, надо сказать, в самых высококультурных очагах - в Греции и Риме, где иным гражданам, особенно знати, очень полюбилось бросание костей и бабок.

Эту страсть переняла Европа, где игры завоевали высокую популярность, и опять же в рядах высшего общества и духовенства. Развлекались столь усердно, что один епископ, не в силах препятствовать греху, решил даже подменить метание костей игрой в "добродетель". Он распорядился вместо цифр на гранях костяшек записать символы добрых дел: "милосердие", "благолепие", "смирение" и т. п. Выигравший должен был наставить в отношении выигранной добродетели того партнера, который ее проиграл.

Наконец появились карты, которые и вовсе разогрели страсти: каков шанс выиграть, какие ставки делать и как их по справедливости поделить? В числе первых ученых, проявивших к азартным играм азарт исследователя, были французский математик Б. Паскаль и итальянский физик и математик Г. Галилей. Это XVII век. Б. Паскаль начал размышлять об идеях теории вероятностей, консультируя неутомимого в карточных делах некоего кавалера де Мере. А однажды друзья попросили подумать над задачей. Два равноценных игрока пожелали прекратить игру раньше срока. В какой пропорции им надлежит разделить банк, если известны счет каждого и ставка игры? Тут пришлось войти в проблему вероятности основательнее.

Что и говорить, сама по себе тема далеко не научная. Но ее решение дает результат, значительно продвигающий науку. Это стало особенно ясным, когда появились работы, посвященные специально проблеме вероятности, то есть проблеме, взятой независимо от карточной игры или игры в кости. Так, в 1812 году вышла первая книга, систематически освещавшая тему. Она была написана авторитетным французским математиком П. Лапласом и называлась "Аналитическая теория вероятности". В ней есть интересное, льющее воду на нашу позицию, признание: "Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее существенным объектом человеческого знания.., Ведь большей частью важнейшие жизненные вопросы являются на самом деле лишь задачами по теории вероятностей".

Теперь уж кто отважился бы объявить (по крайней мере в научной среде) решение задач на вероятность исходов в карточной игре бесполезным для ученого занятием? Тем более делать это после работ Л. Больцано, К. Максвелла (конец XIX столетия), применивших идеи вероятности для описания поведения газов. В XX веке теория пошла еще дальше, и математики умеют ныне "охватить" игру уже вместе с игроками, правилами игры и выигрышами, что вывело ее в ряды методологического "знание добывающего" инструмента с широким, повсеместным полем приложений.