
ГЛАВА 5. ОТ ГАЛИЛЕЯ ДО НЬЮТОНА
ОБЩАЯ МЕХАНИКА
1. РЕНЕ ДЕКАРТ
Изучение физики, согласно Декарту (1596-1650), должно иметь цель сделать людей «господами и хозяевами природы». Этого господства над природой человек может достичь, применив к физическому исследованию методы математики, наиболее совершенной из известных ему наук. Поэтому Декарт поставил себе задачей математизацию физики, или, точнее, ее геометризацию по типу евклидовой геометрии: небольшое число аксиом, само собой очевидных, на которые опирается упорядоченная последовательность выводов, обладающих той же степенью достоверности, что и первичные аксиомы.
Принимая галилееву концепцию вторичных качеств, заключенных не в телах, а в ощущающем субъекте, Декарт кладет в основу своего рассмотрения лишь две сущности - протяженность и движение, которые представляются ему интуитивно понятными, и, будучи убежден в невозможности существования пустоты в природе, наполняет протяженность «тонкой материей», которую бог наделил непрерывным движением.

Рене Декарт. Гравюра неизвестного автора XVII века
Физический мир состоит, таким образом, только из двух сущностей:, материи, простой «протяженности, наделенной формой», лишенной всех качеств, кроме геометрических, и движения. Следовательно, достаточно будет установить законы движения, чтобы вывести затем с помощью ряда последовательных теорем законы чувственного мира.
В своем трактате «Le monde» («Мир») Декарт не упоминает об относительности движения. Но в «Principia philosophiae» («Начала философии»), опубликованных в 1644 г., т. е. после появления «Диалога о двух главнейших системах мира», он, возможно под влиянием этого труда Галилея, принимает принцип относительности, делая все же для осторожности ряд оговорок, позволяющих ему формально не вступать в противоречие с положением о неподвижности Земли, требуемым священным писанием. Но если бы» страх перед инквизицией не заставлял его скрывать свои мысли, Декарт дал бы более широкое понятие относительности, чем Галилей. Действительно, Галилей, а позже Ньютон верили в абсолютное движение по отношению к пространству, тогда как Декарт утверждал относительный его характер. В частной переписке он писал:
«Если из двух человек один движется с кораблем, а второй стоит неподвижно на берегу..., то нет никакого преимущества ни в движении первого, ни в покое второго» (Oeuvres de Descartes, publiees par Charles Adam et Paul Tannery, Paris, 1902, v. VL, p. 348. (Есть русский перевод: Р. Декарт, Избранные произведения, М., 1950.)).
Декартова механика основана на трех законах. Два первых охватывают то, что сейчас называется принципом инерции. Третий закон утверждает постоянство количества движения (произведение массы тела, которую Декарт путал с весом, на его скорость). Декарт полагает также количество движения равным произведению приложенной силы на время ее действия и называет это произведение импульсом силы; это название сохранилось в науке и сейчас в том же значении. Третий закон Декарта является по существу центральным пунктом его механики. То, что Декарт сумел выделить его и положить в основу своей механики, говорит о незаурядной интуиции автора.
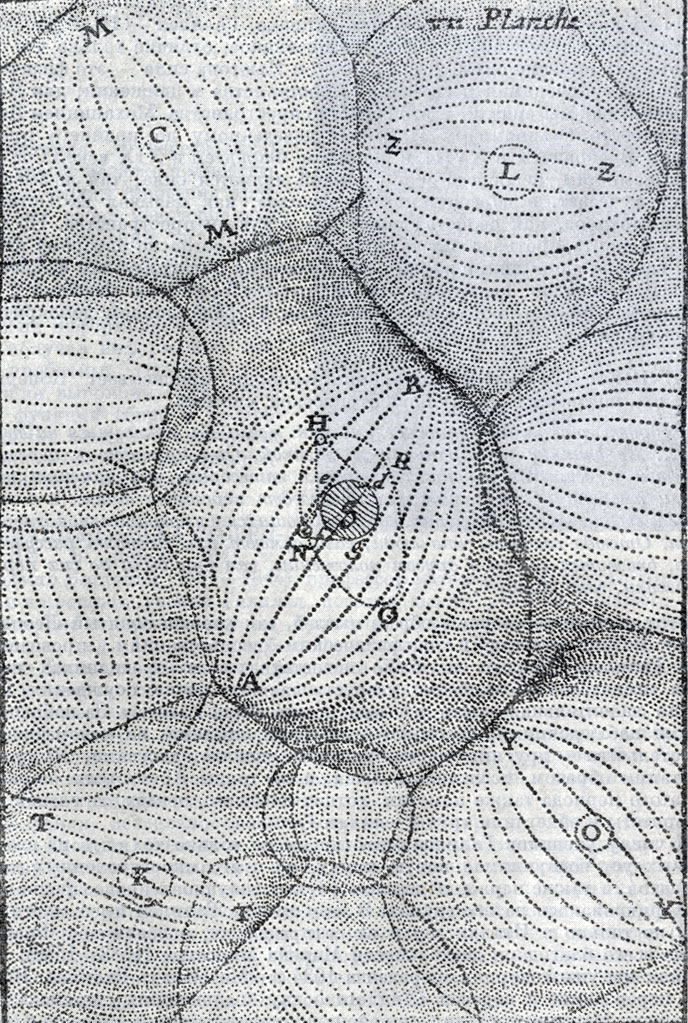
Вихри тонкой материи по представлению Декарта. В центре находится солнечная система. (Oeuvres de Descartes, v. IX.)
К сожалению, в формулировке этого закона Декарт допускает ошибку, весьма странную для геометра его масштаба. Он не учитывает, что поскольку скорость, как мы бы сейчас сказали и как знал Декарт, является вектором, т. е. величиной, имеющей направление и ориентацию, то и количества движения являются векторами, так что их сумму нужно понимать в геометрическом, а не в алгебраическом смысле. Таким образом, формулировка третьего закона ошибочна. Отсюда неверность вытекающих из него семи правил (за исключением первого), образующих декартову теорию соударения упругих тел.
Некоторые случаи соударения, исследованные Декартом, легко проверяются на опыте. Например, четвертое декартово правило гласит, что если неподвижное тело испытывает центральное соударение с другим телом меньшей массы, то оно остается неподвижным, тогда как движущееся тело меняет направление скорости на обратное с сохранением абсолютной величины скорости. Но достаточно подойти к бильярдному столу, чтобы убедиться в ошибочности этого правила. И Декарт действительно это сделал и установил неверность своих правил. Но он слишком доверял своему разуму и своим «ясным и четким» идеям. Опыт опровергает теоретические построения? Тем хуже для опыта. Опыт не удается, говорит с уверенностью Декарт, потому что эти правила предполагают,
«что тела идеально твердые и настолько удалены от всех остальных тел, что ни одно из этих тел не может способствовать или препятствовать их движению» (Oeuvres de Descartes, v. IX, p. 93).
Но даже если признать это объяснение правильным, как же мы сможем стать хозяевами природы, располагая физикой, говорящей о явлениях имеющих место в ином мире, а не в том, в котором мы существуем?
Установив законы движения, Декарт в трактате «Мир» и в «Началах философии» начинает свой космологический роман, объясняя образование Солнца, планет, комет. Наконец, он спускается с неба на Землю и устанавливает, что тонкая материя обладает тремя действиями: светом, теплом и тяготением. Этим он создает основы того представления о флюидах, которое господствовало в физике в течение всего XVIII и частично в XIX веке. Эти удобные флюиды, которые, подобно добрым гномам, готовы к услугам в наиболее трудных случаях и скромно действуют скрытно от наших чувств, не представляют ли они, по крайней мере частично, возврат назад, к оккультизму? По нашему мнению, это так.
Но всегда нужно помнить, что представление о флюидах оказало физике также громадные услуги, особенно в оптике и теории электричества. При этом мы имеем в виду научную концепцию, временное модельное представление, инструмент механистической философии, но не конкретные флюиды, введенные Декартом, как, например, его магнитный флюид, состоящий из двух типов частиц спиральной формы с тремя витками, навитыми в противоположные стороны. С его помощью Декарт дал ответ на 34 вопроса, которые можно, по его мнению, задать по магнетизму. Этот магнитный флюид и эта вызывающая восхищение цепь рассуждений на протяжении всех «Начал» свидетельствуют об искусстве Декарта в построении гипотетических дедуктивных систем, но ни на йоту не обогащают наших знаний о магнитных явлениях.
Совсем иную роль сыграло декартово понятие тяжести. Каждое тело находится, по Декарту, в вихре, будучи окруженным в свою очередь другими вихрями, которые прижимают его к центру. Это стремление к центру и составляет вес тела, т. е. тяжесть. Если бы Галилей это знал, сказал Декарт в известном письме к Мерсенну, ему не нужно было бы строить безосновательную теорию падения тел в пустоте.
Письмо Декарта, которое мы уже упоминали выше, представляет собой резкую критику «Беседы, касающейся двух новых отраслей науки» Галилея и интересно с точки зрения различия мышления обоих ученых: для Декарта физика должна искать ответ на вопрос, почему происходят явления, по Галилею - исследовать, как они происходят; поиски причины - цель Декарта, описание явлений - цель Галилея. В вопросе падения тяжелых тел Декарт не соглашался с законами Галилея и не понимал их, в частности, потому, что его кинематике было чуждо понятие ускорения.
Вес, как и любую силу, Декарт понимал как реакцию связей геометрического типа. Это - свойство движения тонкой материи. Так что, отождествляя ее с пространством и пользуясь более понятной сейчас терминологией, можно сказать, что вес есть свойство пространства. Но к такому пониманию картезианство никогда не склонялось, и потому оно пало, побежденное приверженцами ньютонова притяжения, несмотря на защиту со стороны Гюйгенса и Лейбница, которые обратили внимание на то, что ньютоново понимание притяжения, воспринявшее кеплерово понятие prensatio или vis prensandi, заключенной в теле, представляет собой неявное возвращение к оккультным свойствам схоластики, потому что в конце концов, для того чтобы тело А притягивало тело 5, нужно, чтобы оно знало, где находится тело В.
Обычно говорят, что декартово понимание физики механистично. Но понимание Галилея и Ньютона тоже было механистичным, потому что под механицизмом понимаются все иногда противоречащие друг другу теории, которые объясняют все физические явления с помощью системы движений, подобных движению механизма. Нам представляется, что механицизм Декарта отличается от механицизма Галилея - Ньютона двумя существенными чертами. Первое, более очевидное, отличие только что отмечалось - это понятие силы. Для Галилея и Ньютона сила - это физическая реальность, не сводимая к свойствам пространства и движения; для Декарта же сила, как мы видели, - это свойство пространства. Механицизм Декарта противостоит динамизму Ньютона, доведенному до крайнего предела Рожером Босковичем в XVIII и Майклом Фарадеем в XIX веке. Согласно этим динамистам, непосредственно данной является сила; так называемая материя исчезает, а ее «почтенные качества», как называл их Оствальд, суть не что иное, как свойства полей сил в пустом пространстве. Но механицизм Декарта противостоит также и атомизму, согласно которому именно атомы создают поля сил, а их скрытые движения объясняют все физические процессы. Очевидно, декартово учение, отождествляющее вещество с протяженностью, не могло быть атомистическим в традиционном демокритовом смысле слова.
2. УЧЕНИКИ ГАЛИЛЕЯ
Джакомо Леопарди приписывает Копернику слова, что подтверждение гелиоцентрической системы
«... не будет таким простым делом, как могло бы показаться на первый взгляд... Ее влияние не ограничится физикой. Она приведет к переоценке ценностей и взаимоотношений различных категорий] она изменит взгляд на цели творения. Тем самым она произведет переворот также и в метафизике и вообще во всех областях, соприкасающихся с умозрительной стороной знания. Отсюда следует, что люди, если сумеют или захотят рассуждать здраво, окажутся совсем в другом положении, чем они были до сих пор или воображали, что были» (Giacomo Leopard i, Le operette morali, Livorno, 1870, p. 314, с предисловием Пьетро Джордани, издание исправленное и дополненное Дж. Кьярини).
Этот полный переворот в образе мыслей, так хорошо понятый Леопарди, вполне можно отнести и к физическим исследованиям, проведенным после Галилея. Правда, не было недостатка и в противниках нового метода исследования, особенно усердствовавших после осуждения Галилея, но значительная часть их вынуждена была отвечать на наблюдения другими наблюдениями, на опыты - другими опытами, на математические доказательства - другими математическими доказательствами. Вынужденные, таким образом, исследовать вещи, а не труды Аристотеля, перипатетики этого периода также помогли, хотя и косвенно, отказу от слепой веры в авторитеты и облегчили труд ученикам Галилея.
К числу учеников Галилея мы относим не только тех, кто из его собственных уст воспринимал новую науку, но и его многочисленных корреспондентов, а также первое поколение ученых, научное мировоззрение которых формировалось на его трудах. В этом смысле Галилей имел много учеников не только в Италии, но и за ее пределами, особенно во Франции, прежде всего благодаря деятельности Марена Мерсенна (1588-1648), который, как мы уже говорили, перевел в 1634 г. «Механику» Галилея. Позже, когда переиздание и перевод «Диалога о двух главнейших системах» были запрещены, Мерсенн составил для своих соотечественников краткое изложение этой работы и распространил во Франции исследования Галилея по падению тяжелых тел; он был первым среди ученых того времени, кто поддерживал точку зрения о субъективном характере ощущений. Хотя в труде Мерсенна мы бы напрасно искали оригинальные идеи, он все же сыграл важную роль в распространении новой науки, информируя о работах других ученых, комментируя и пересказывая их, а иногда издавая полностью. Поэтому труды Мерсенна представляют собой неисчерпаемый источник сведений об уровне знаний в ту бурную эпоху. Неутомимый корреспондент крупнейших ученых того времени, Мерсенн информировал других, сам получал информацию, ставил проблемы, выдвигал возражения, выполняя, таким образом, функции сбора и распространения знаний, возложенные сейчас на большие международные научные журналы.
3. ЭВАНДЖЕЛИСТА ТОРРИЧЕЛЛИ
В апреле 1641 г. Бенедетто Кастелли (1577-1644), профессор математики Римского университета и в прошлом ученик Галилея, посетил своего учителя, жившего тогда в Арчетри, и привез ему на просмотр рукопись о движении свободно падающих тел. Ее автором был Эванджелиста Торричелли (1608-1647), ученик Кастелли. Кастелли предложил Галилею взять Торричелли к себе в дом в качестве помощника в подготовке исследований по механике. Получив согласие Галилея, Торричелли в первой половине августа того же года переехал к нему в Арчетри. Но их сотрудничество продолжалось всего три месяца. Галилей умер. Великий герцог Тосканский, прибывший в Арчетри в связи со смертью Галилея, назначил Торричелли на ставшую вакантной должность придворного математика.

Эванджелиста Торричелли
Научная деятельность Торричелли, бесспорно, самого блестящего ученика Галилея, относится к области физики и математики. Однако, следуя примеру своего учителя, он не гнушается и практической деятельности. Узнав от Галилея о значении изготовления линз и подзорных труб, он с 1642 г. стал упорно заниматься этим и вскоре достиг такого совершенства, что намного превзошел наиболее знаменитых итальянских мастеров (Ипполита Мариани, прозванного «Простофилей», Евстахия Дивини из Рима, Франческо Фонтана из Неаполя), изделия которых признаются крупнейшими достижениями оптики первой половины XVII века.
В дальнейшем мы будем говорить об открытии Торричелли атмосферного давления, открытии, которое больше других способствовало тому, что его имя стало бессмертным. Сейчас мы ограничимся лишь кратким рассмотрением его работ по механике, содержащихся в единственной опубликованной им книге, состоящей из трех частей. Первая и третья части посвящены геометрии, а вторая, озаглавленная «De motu gravium descendentium et proiec-torum libri duo» («О движении свободно падающих и брошенных тяжелых тел»), представляет собой ту рукопись, которую Кастелли принес на просмотр Галилею.
В первой книге этого трактата Торричелли ставит себе целью доказать постулат Галилея о равенстве скоростей тяжелых тел, падающих по наклонным плоскостям одинаковой высоты, и, не зная, что это уже сделано Галилеем, доказывает его. При этом он принимает в качестве постулата принцип, носящий сейчас имя Торричелли, о движении центров тяжести. Благодаря Торричелли при многочисленных применениях этого принципа (к наклонной плоскости, рычагу, движению по хорде круга и по параболе) были опровергнуты взгляды ряда авторитетных ученых, которые ставили в упрек Архимеду то, что он считал вертикальные направления двух нитей с подвешенными грузами у поверхности земли параллельными, а не сходящимися к центру Земли. Торричелли показал, что представление Архимеда более пригодно для теоретических физических исследований.
Во второй книге трактата Торричелли сначала рассматривает движение брошенных тел, обобщая подход, принятый в «Беседах» Галилея, где обсуждается лишь движение тел, брошенных по горизонтали. Только попутно, для доказательства, Галилей выдвинул утверждение, что если тело бросить из точки его падения со скоростью, равной, но противоположной той, с которой оно пришло в точку падения, то оно пройдет ту же параболу в обратном направлении. Торричелли же рассмотрел движение тела, брошенного под произвольным углом, и, применив к нему принципы Галилея, определил параболический характер траектории и установил другие, хорошо известные сейчас теоремы баллистики. В частности, обобщая наблюдение Галилея, он заметил, что движение брошенного тела - явление обратимое. Таким образом, представление о том, что динамические явления обратимы, т. е. что время в галилеевой механике упорядочено, но лишено ориентации, восходит к Галилею и Торричелли.
После раздела «О движении жидкостей», которого мы коснемся ниже, Торричелли приводит пять баллистических таблиц, по-видимому, первых таблиц в истории артиллерии, причем, опасаясь, что практики, для которых предназначены эти таблицы, не понимают латыни, он внезапно переходит на итальянский язык.
В вопросе о движении жидкостей (непосредственными предшественниками в этих исследованиях были Бенедетти и Кастелли) вклад Торричелли столь велик, что Мах провозгласил его основателем гидродинамики. Основная проблема, которую поставил перед собой Торричелли, заключалась в определении скорости истечения жидкости из узкого отверстия в дне сосуда. С помощью специального приспособления он заставил жидкость, вытекающую из отверстия, бить ключом вверх и установил, что она подымается на высоту, меньшую, чем уровень воды в сосуде. Тогда он предположил, что, если бы совсем не было сопротивления движению жидкости, струя поднялась бы до уровня воды в сосуде. Очевидно, эта гипотеза эквивалентна для данного частного случая закону сохранения энергии. Используя аналогию с падением тяжелых тел, Торричелли выводит из принятой гипотезы следующее основное положение (называемое теперь «теоремой Торричелли»):
«Вырывающаяся из сосуда вода имеет в точке истечения ту же скорость, которую имело бы произвольное тяжелое тело, а значит, и отдельная капля той же воды, падая свободно с верхнего уровня этой воды до уровня отверстия» («De motu...», Libro II, prop. XXXVII, в книге Ореrе di Evangelista Torricelli, ed. G. Loria, G. Vassura, Faenze, II, 1919, p. 186).
Эта теорема, являющаяся основой гидростатики, была впоследствии доказана Ньютоном и Вариньоном. Торричелли испо.льзовал ее вместе с уже полученными результатами, касающимися движения брошенных тел, чтобы доказать, что если отверстие сделано в стенке у дна сосуда, то струя имеет параболическую форму. Кроме того, Торричелли принадлежат тонкие физические наблюдения над распадением на капли струи жидкости и влиянием сопротивления воздуха.
4. ДЖОВАННИ АЛЬФОНСО БОРЕЛЛИ
К ученикам Галилея относится также неаполитанец (по другим данным - мессинец) Джованни Альфонсо Борелли (1608-1679) - один из наиболее проницательных умов итальянской науки XVII века. Борелли предвосхитил ньютоново представление о том, что планеты стремятся к Солнцу по той же причине, по которой тяжелые тела стремятся к Земле. Его сравнение движения камня, вращающегося на краю пращи, и движения планеты вокруг Солнца, по почти единодушному мнению всех критиков, - первый зародыш теории динамического равновесия движущихся планет. Согласно Борелли, «инстинкт», который заставляет планету стремиться к Солнцу, уравновешивается тенденцией каждого тела удаляться от центра. Борелли считает эту vis repellens, или центробежную силу, как мы ее сейчас называем, обратно пропорциональной радиусу описываемой окружности.
В своей работе по механике «De vi percussionist («0 силе удара»), 1667 г., более широкой по смыслу, чем это видно из названия, он приводит законы центрального соударения двух неупругих сфер, справедливые и сейчас. В этой работе он ставит себе целью определить, каково было бы эффективное движение падающих тел, если предположить (ex mera hypothesi - «чисто гипотетически», добавляет он с осмотрительностью, особенно необходимой, поскольку он был монахом), что тела принимают участие в равномерном круговом вращательном движении Земли. И он приходит к выводу об отклонении тел к востоку, которое было экспериментально подтверждено лишь в 1791 г. Джован Баттистой Гульельмини (?-1817) в опытах с падением тел с башни Азинелли в Болонье.
В своей работе «De motionibus naturalibus a gravitate pendentibus» («О естественных движениях, зависящих от тяжести»), 1670 г., одну главу он посвящает экспериментальному исследованию капиллярных явлений и приходит к выводу, что в капиллярных трубках подъем жидкости обратно пропорционален диаметру трубки. Этот закон был вторично открыт в 1718 г. врачом Жаком Жюреном (1684-1750), по имени которого он и назван. В этой же работе приведено определение удельного веса воздуха - с помощью прибора - первого представителя ареометров с постоянным объемом. В 1656 г. Борелли вместе с Вивиани определили скорость звука в воздухе, воспользовавшись прямым методом, предложенным Галилеем, т. е. измеряя интервал времени между моментом светового восприятия взрыва и моментом, когда становится слышен звук взрыва. Так ему удалось получить значительно более точные результаты, чем его предшественникам (Мерсенн, Гассенди и др.). Однако лучшим творением Борелли, достойно венчающим все остальные его работы, является его труд «De motu animalium» («О движении животных»), вышедший посмертно в двух томах в 1680- 1681 гг. в Риме, где Борелли умер в глубокой нищете.
В первом томе описываются строение, форма, действие и возможности мышц человека и животных. Во втором томе с помощью механических аналогий рассматриваются сокращения мышц, движения сердца, циркуляция крови, пищеварение. Эта работа, многократно переиздававшаяся, положила начало новому научному направлению - ятромеханике. Особенное восхищение вызывает глава XXII о полете птиц (De volatu), издававшаяся поэтому много раз отдельно. Уже в нашем веке в английском переводе эта глава была включена в серию «Aeronautical classics» (№ 6, London, 1911), а в немецком переводе - в серию «Klassiker der exakten Wissenschaften» (№ 221, Leipzig, 1927).
5. МАЯТНИКОВЫЕ ЧАСЫ
Вскоре после открытия «медицейских планет», т. е. первых четырех спутников Юпитера (Галилей назвал обнаруженные им спутники Юпитера «медицейскими звездами» в честь герцога Тосканского Козимо Медичи. - Прим. перев), у Галилея родилась идея использовать их для определения долготы места, что, как известно, имеет громадное значение для мореплавателей. Теоретически определение долготы выглядит весьма просто: рассчитав для какого-то места эфемериды, определяющие момент, когда спутник входит в конус тени Юпитера, достаточно установить время, когда это явление наблюдается в другом месте, чтобы по разности этих времен найти разность долгот обоих мест. Но применение этого метода требует таблиц с эфемеридами и двух хронометров.
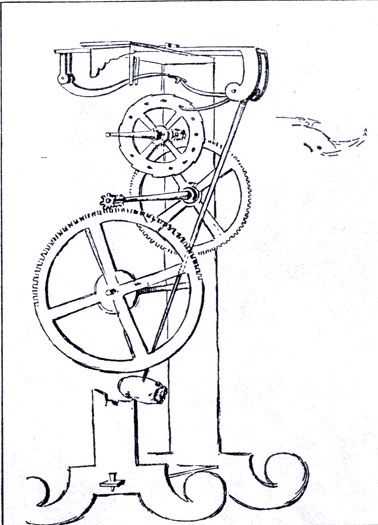
Часы с маятником Галилея на рисунке В. Вивиани. (Le opere di Galileo Galilei, v. XIX.)
В 1612, затем в 1616 г. и еще позже в 1630 г. Галилей пытался вступить в переговоры с испанским правительством, чтобы передать ему это открытие, но его попытки не увенчались успехом. В 1636 г. он вновь обратился с этим предложением к Генеральным штатам Нидерландов, которые с удовольствием приняли это предложение, тотчас назначили специальную комиссию для его рассмотрения и постановили отправить в дар Галилею золотое колье стоимостью 500 флоринов. Комиссия отметила некоторые недостатки проекта Галилея, которые тот признал справедливыми, но вполне преодолимыми. Однако дело было не из тех, которые можно решить перепиской, поэтому Галилей предложил, чтобы к нему в Арчетри приехали представители Генеральных штатов. Друзья Галилея обратились к секретарю принца Оранского Константину Гюйгенсу, отцу Христиана Гюйгенса, с просьбой оказать содействие, используя свое высокое положение при Генеральных штатах. Константин Гюйгенс принял предложение и довел переговоры до благополучного конца. Однако весть о них дошла до кардинала Франческо Барберини, и тот немедленно приказал Генеральному инквизитору Флоренции воспрепятствовать переговорам. Поэтому Галилей прервал переговоры и отказался от дара Генеральных штатов, который как раз в эти дни ему доставила купеческая делегация.
15 августа 1636 г. во время переговоров Галилей писал Генеральным штатам:
«У меня есть такой измеритель времени, что если бы сделать 4 или 6 таких приборов и запустить их, то мы бы обнаружили (в подтверждение их точности), что измеряемое и показываемое ими время не только из часу в час, но изо дня в день, из месяца в месяц не отличалось бы на различных приборах даже на секунду, настолько одинаково они бы шли» (Le Opere di Galileo Galilei, Ediz. Naz., XVI, p. 467).
Нетрудно сообразить, что измеритель времени, о котором упоминает Галилей, должен был быть прибором, в котором используется изохронизм колебаний маятника. И действительно, в письме от июня 1637 г. Реалю (или Реалио - согласно принятому итальянизированному написанию), губернатору Голландских Индий, Галилей сообщает, что его часы представляют собой применение маятника, и описывает также специальный счетчик числа колебаний. В 1641 г., по словам Вивиани, ему
«... пришло в голову, что можно добавить маятник к часам с гирями и с пружиной» (Там же, XIX, p. 655).
Уже глубоким стариком он поверил эти планы своему сыну Винченцо (ум. в 1649 г.). Отец и сын решили построить механизм (дошедший до нас благодаря чертежу Вивиани) с остроумным устройством часового спуска (так называемый «крючковый спуск»). То, что Винченцо Вивиани построил в действительности такие часы, установлено точно: это следует из инвентарной описи наследства его жены и из переписки Леопольдо де Медичи, который послал Буйо 21 августа 1659 г. чертеж модели, «нарисованный столь же грубо, как и сама модель, находящаяся сейчас в моей комнате».
Христиан Гюйгенс (1629-1695) в письме от 12 января 1657 г. сообщил о созданных им маятниковых часах. В июне того же года он получил патент на эти часы, а в 1658 г. опубликовал свое открытие в сочинении «Horologium» («Часы»). Знал ли о проекте Галилея Христиан Гюйгенс, сын Константина Гюйгенса, принимавшего большое участие в переговорах Галилея с Генеральными штатами и, в частности, знакомого с идеей Галилея о применении маятника в часах? Он всегда отрицал это, признавая лишь, что ему пришла в голову та же идея, что и Галилею, часы которого шли так же хорошо, как и его собственные, и говорил, что целью создания часов он, как и Галилей, считал определение долготы места на море.
Мы не видим оснований не доверять голландскому ученому, конструкция часов которого уступает конструкции Галилея в механизме спуска, так как он сохранил старинное несовершенное устройство, но зато значительно превзошел Галилея, заменив гирю пружиной с балансом.
6. ХРИСТИАН ГЮЙГЕНС
Опубликование «Часов» вскоре создало Гюйгенсу такую славу, что Кольбер пригласил его в 1666 г. в Париж, где в то время была основана Парижская Академия наук (см. § 14). Там Гюйгенс оставался до 1681 г. Осложнившаяся обстановка в связи с преследованиями гугенотов, к которым принадлежал Гюйгенс, заставила его благоразумно вернуться в Гаагу.
Его работа 1658 г. о часах носит ясно выраженный прикладной характер. Но от математика такого масштаба, как Гюйгенс, не укрылись и те теоретические проблемы механики, которые связаны с созданием часов. Исследованию этих проблем он посвятил последующие годы. В 1673 г. в Париже выходит его шедевр - труд «Horologium oscillatorium, sive de motu pendulorum ad horologia aptato demonstrationes geometricae» («Качающиеся часы, или о движении маятника»), состоящий из пяти частей: описание часов, движение тяжелых тел по циклоиде; развертка и определение длины кривых линий; центр колебаний или возбуждения; устройство другого типа часов - с круговым маятником; теоремы о центробежной силе.

Христиан Гюйгенс
Гюйгенс был прямым продолжателем Галилея и Торричелли, теории которых он, по его собственному выражению, «подтверждал и обобщал». Галилей основал динамику лишь одного тела, Гюйгенс же начал построение динамики нескольких тел.
Остановимся вкратце на содержании этой работы, имеющей фундаментальное значение для истории механики, опустив при этом первую и третью части, не имеющие прямого отношения к нашей теме.
Во второй части, после изложения галилеевских законов падения тяжелых тел, доказательство которых он уточняет систематическим применением принципа сложения перемещений, Гюйгенс с помощью замечательных рассуждений дифференциально-геометрического характера устанавливает изохронизм колебаний циклоидального маятника.
Четвертая часть начинается с упоминания о том, что в те годы, когда Гюйгенс был еще юношей, Мерсенн предложил ему найти центр колебаний, т. е. уточку на проведенном через центр тяжести перпендикуляре к оси колебаний, отстоящую от оси колебаний на расстоянии, равном длине простого маятника, изохронного с данным сложным маятником.
Понятие центра колебаний, которому Гюйгенс дал приведенное выше определение, встречается уже у Галилея и повторяется у Мерсенна в 1646 г.: если бы имелась совокупность простых маятников различной длины, представляемых как тяжелые точки, подвешенные на невесомых нитях так, что все были бы прикреплены к одной и той же перекладине, то более короткие маятники колебались бы быстрее более длинных. Если все эти маятники сразу скрепить между собой так, чтобы они образовали жесткую систему, то они вынуждены были бы все совершать колебания за одно и то же время, более короткие маятники ускоряли бы движение более длинных, одни маятники теряли бы скорость, другие увеличивали бы ее, а третьи не теряли бы и не увеличивали. Центром колебаний называется положение тяжелой точки того из маятников этой последней группы, который расположен на перпендикуляре к оси подвеса, проведенном через центр тяжести.
Руководствуясь приведенными соображениями, Декарт и Роберваль пытались найти положение центра колебаний, но эта попытка успехом не увенчалась.
Гюйгенс также занялся этой проблемой и решил ее, приняв за основу рассмотрения принцип Торричелли. Теория Гюйгенса представлялась его современникам неубедительной, поэтому Якоб Бернулли развил в 1703 г. другую, более строгую теорию и пришел к той же формуле для «приведенной длины» сложного маятника, что и Гюйгенс. В ходе рассмотрения проблемы было введено понятие момента инерции и было открыто знаменитое соотношение (предложение XX у Гюйгенса): «центр колебаний и точка подвеса «взаимосопряжены» (Ch. Huуgens, Horologium oscillatorium, Paris, 1673, в книге Oeuvres completes, XVIII, La Haye, 1934, p. 305).
Это соотношение позволяет находить центр колебаний экспериментально. В 1818 г. Генрих Катер (1777-1835) использовал эту теорему, сконструировав «обратимый маятник», т. е. практический прибор для определения длины секундного маятника и для определения значения ускорения силы тяжести в данном месте. И этим последним применением маятника мы тоже обязаны Гюйгенсу.
В 1676 г. Жан Рише (ум. в 1696 г.) был чрезвычайно удивлен тем, что маятник с секундным периодом в Париже стал в Кайенне колебаться медленнее. Его укоротили и после окончания исследований перевезли обратно в Париж, где он, наоборот, стал колебаться быстрее. Гюйгенс в своем труде «Duscours sur la cause de la pesanteur» («О причине тяжести»), законченном в 1681 г. и опубликованном в 1690 г., объяснил это явление изменением значения ускорения силы тяжести, которое он приписывал исключительно вариации центробежной силы, обусловленной вращением Земли. Это исследование привело его к заключению, что Земля должна быть сплющена у полюсов ж вздута у экватора. Чтобы подтвердить это экспериментально, он привел в быстрое вращение шар из мягкой глины, надетый на ось, и наблюдал его сплющивание. Как известно, сейчас этот опыт повторяется в учебных целях с упругими стальными кольцами, надетыми на ось по диаметру. Этот опыт оказал заметное влияние на генезис космогонических теорий Канта и Лапласа.
С 1659 г. Гюйгенс писал трактат «De vi centrifugal («О центробежной - силе»), который был опубликован лишь посмертно, в 1703 г. В нем Гюйгенс исследовал «стремление» (conatus) тела, прикрепленного к вращающемуся колесу, - это стремление, согласно Гюйгенсу, той же природы, что и стремление тяжелого тела к падению. Что произойдет, если человек, находящийся на вращающемся колесе, держит в руке нить, на которой висит свинцовый шарик? Произойдет то, отвечает Гюйгенс, что нить будет натянута с такой же силой, которая тянула бы шарик, если бы он был прикреплен к центру .колеса. После некоторых геометрических рассуждений Гюйгенс приходит к выводу:
«Conatus шара, прикрепленного к вращающемуся колесу, таков, что шар -стремился бы двигаться равномерно ускоренно по радиусу... Этот conatus аналогичен тому, который имеется у тяжелого тела, подвешенного на нити. Отсюда мы заключаем, что центробежные силы неодинаковых тел, движущихся с одинаковой скоростью по равным окружностям, относятся между собой как веса этих тел, т. е. как количества вещества в них... Остается найти величину или количество conatus для различных скоростей вращения» (Ch. Huуgens, De vi centrifuga, в книге Oeuvres completes, XVI, 1929, p. 266).
Остается добавить, что определяющие центробежную силу законы, найденные Гюйгенсом и приведенные без доказательства в конце «Качающихся часов», совпадают с теми, которые мы можем сейчас прочесть (с небольшим изменением терминологии) в любом элементарном курсе физики.
После нашего беглого обзора излишне добавлять, что для Гюйгенса центробежная сила отнюдь не фиктивная, а вполне реальная сила той же природы, что и сила тяжести.
О работах Гюйгенса по оптике мы будем говорить в следующей главе. В эту область голландский ученый внес наибольший вклад. Однако мы не можем закончить обзор его работ по механике, не упомянув об исследованиях столкновений тел.
Эта задача представляла особую трудность для первых механиков. Ею занимался Джован Баттиста Бальяни в своей работе «De motu gravium, solidorum» («0 движении твердых тел»), 1638 г. Галилей собирался посвятить, этому вопросу «День шестой» своих «Бесед», но хотя в дошедших до нас фрагментах могут вызвать восхищение удивительно интересные эксперименты, никакого решения проблемы мы там не найдем. Как мы видели ранее, на этом подводном камне потерпела крушение вся механика Декарта. Значительно больше повезло Борелли, который нашел законы соударения неупругих тел. Гюйгенс же обратился к исследованию соударения упругих тел.
В своей работе «De motu corporum ex percussione» («О движении тел после удара»), законченной в 1656 г., но опубликованной уже после его смерти, в 1700 г., Гюйгенс рассматривает эту сложную задачу на основе трех принципов: принципа инерции, принципа относительности и третьего принципа, о котором мы скажем ниже. Здесь же мы добавим, что принцип относительности Гюйгенс понимает в смысле Декарта, т. е. более широко, чем Галилей и Ньютон; иными словами, Гюйгенс не признает абсолютного движения относительно пространства.
Третий принцип (по нумерации Гюйгенса - второй) утверждает, что если два одинаковых тела с равными, но противоположно направленными скоростями испытывают центральный удар, то они отлетают одно от другого с теми же скоростями, но измененившими знак. Основываясь на этих исходных принципах, Гюйгенс вывел законы соударения упругих тел, которые затем изложил в мемуаре, представленном в 1669 г. на конкурс на лучшую работу по теории удара, объявленный Королевским обществом годом раньше. В этом конкурсе участвовали также Джон Уаллис (1616-1703), рассмотревший соударение неупругих тел, и Христофор Рен (1632-1723), рассмотревший соударение упругих тел. Исследование Гюйгенса, несомненно, значительно превосходило эти две работы и по широте постановки вопроса и по ясности изложения; правда, иной раз ясность достигалась в ущерб краткости. Последующие исследования по механике мало что изменили в законах соударения Гюйгенса.
В работах Уаллиса, Рена и Гюйгенса изложение носит геометрический характер. Эдм Мариотт (1620-1684) в своей работе «Traite de la percussion ou choc des corps» («Трактат о соударении тел»), опубликованной посмертно в его трудах (Лейден, 1717), исследовал те же задачи и чисто экспериментальным путем пришел примерно к тем же результатам. Чтобы иметь возможность произвольно регулировать скорость тела, Мариотт придумал приспособление, состоящее из двух равных маятников, которые можно заставить падать с произвольно регулируемой высоты. Ему принадлежит также прибор, применяемый и сейчас для демонстрации передачи движения упругими телами и состоящий из ряда подвешенных на нитях упругих шаров, соприкасающихся друг с другом; если сместить первый шар и позволить ему падать, то последний шар поднимется вверх, а остальные останутся неподвижными.
7. ПОЛЕМИКА О ЖИВОЙ СИЛЕ
В упомянутой выше работе о соударении тел и в более явной форме еще раз в 1686 г. Гюйгенс выдвигает утверждение, что сумма произведений «каждого тела» на квадрат его скорости до и после удара остается неизменной. С этой теоремой сохранения был знаком и Лейбниц, который, сообщив о ней письмом Гюйгенсу, сделал ее предметом мемуара «Demonstratio erroris memorabilis Cartesii» («Доказательство примечательной ошибки Декарта»), опубликованного в 1686 г. в «Acta eruditorum» («Ученые записки»). В этом мемуаре Лейбниц называет произведение «тела» на квадрат его скорости «живой силой» и противопоставляет его «мертвой силе», или, как мы бы ее назвали теперь, потенциальной энергии. Первое выражение, как известно, осталось в науке до сих пор с изменением, внесенным Густавом Кориолисом (1792-1843), который в качестве меры живой силы предпочел принять половину произведения массы тела на квадрат его скорости.
Итак, Лейбниц предложил оценивать «силу» (мы бы сказали - энергию) падающего тела высотой, на которую это тело могло бы подняться, если бы его бросили вверх с приобретенной им скоростью; таким образом, во всех случаях имело бы место равенство между живой силой и мертвой силой. Если так оценивать «силу», то из законов механики можно вывести, что она равна произведению «тела» на квадрат его скорости, так что тело, удвоившее свою скорость, учетверяет свою «силу». При соударении тел сохраняется не количество движения, как утверждает третье правило Декарта, а сумма живых сил соударяющихся тел; в этом, согласно Лейбницу, и кроется ошибка Декарта.
Однако картезианцы поднялись против Лейбница в защиту Декарта. Между сторонниками Лейбница и Декарта завязались оживленные споры, длившиеся свыше 30 лет и известные в истории физики как «полемика о живой силе».
По сути дела, картезианцы обращали внимание на то, что когда тело, брошенное вверх, подымается на первоначальную высоту за вдвое большее время и производит учетверенный эффект за вдвое большее время, то это означает, что его «сила» не учетверилась, а лишь удвоилась. Здесь неуместно входить в технические детали полемики. Достаточно сказать, что спор был разрешен в 1728 г. Жан-Жаком де Мераном (1678-1771) и еще лучше Жаном Даламбером (1717-1783) в предисловии к его «Traite de dynamique» («Трактат о динамике»), 1743 г. Весь спор был основан на двусмысленности определения количества движения. Картезианцы придерживались скалярного определения, данного Декартом. Де Меран показал, что все примеры соударений, приведенные в процессе полемики, подчиняются закону сохранения количества движения, если только его понимать правильно, т. е. в векторном смысле. Таким образом, окончательно: при упругом ударе имеет место как сохранение количества движения, так и сохранение живой силы
http://housekvar.ru/dizayn/ustanovka-mezhkomnatnoj-dveri-pravila-i-sovety.html
|
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'