
ПЕСТРЫЙ МИР КАЛЕЙДОСКОПА
Не знаю, милый читатель, был ли у вас в детстве калейдоскоп, но если нет, то что-то безвозвратно прошло мимо вас... Калейдоскоп - это трубка, глядя в которую вы видите фантастически прекрасный узор из разноцветных многоугольников. Стоит повернуть игрушку, как внутри послышится легкий шорох и возникнет новый орнамент. И так при каждом повороте, и всякий раз новый узор - один неожиданней и красивее другого.
Детская любознательность не ведает границ. Ребенку так интересно узнать, как и почему появляются все новые и новые фигуры, что он разбирает трубочку на части (благо она из картона). И сколь велико бывает разочарование, когда внутри обнаруживается всего-навсего несколько разноцветных осколков стекла и бусинок да еще два маленьких зеркальца...

Из-за преломления света удильщик видит щуку не там, где она находится на самом деле
Если вы никогда не заглядывали в калейдоскоп, вспомните «заставки», появляющиеся на экране вашего телевизора в паузах рекламных передач. Эти меняющиеся геометрические орнаменты напоминают узоры калейдоскопа.
Принцип действия калейдоскопа наглядно демонстрирует простой эксперимент. Поставьте два зеркала под углом друг к другу, поместите перед ними свечу, и вы увидите четыре свечи. Ведь в зеркальном угле с раствором 90° наблюдаемый предмет виден четырежды (360° : 90° = 4):один раз в оригинале и трижды - в отражениях. Зеркальный угол с раствором 72° покажет то же изображение 5 раз. А два зеркала, угол между которыми составляет 60°, дадут нам шестикратное изображение. Разница между великолепным многоцветным узором и скромной действительностью с ее двумя небольшими зеркалами н четырьмя-восемью маленькими бусинками и осколками цветного стекла ошеломляет!
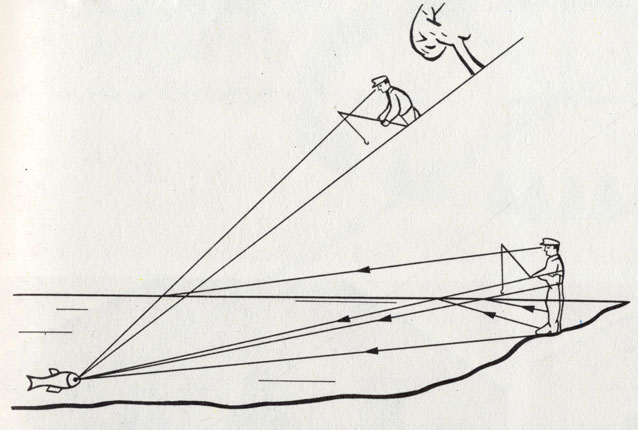
В соответствии с законами оптики рыба может (вероятно) видеть стоящего в воде рыбака парящим в воздухе
В одной старой книге содержится прекрасное описание опыта, оно так удачно, что заслуживает внимания и современного читателя.
«Картина, увиденная под водой. Пословицу «не всему верь, что слышишь», следовало бы продолжить, прибавив утверждение, что нельзя принимать за правду все, что видишь. Из всех оптических обманов нет более невероятного, более поразительного, чем зрелище рыбака, каким его видит рыба».
Рассмотрим сначала обратный случай: как удильщик видит щуку. Луч его зрения преломляется на поверхности воды. Голландец Снеллиус, с которым мы уже познакомились, рассматривая падающие на зеркало и отраженные от него лучи, открыл в 1620 г. закон преломления. Он показал, что луч света, проходящий через две прозрачные среды (воздух, вода), изменяет свое направление на определенный угол, Величина этого угла зависит от отношения показателей преломления обеих сред и от угла падения луча. В виде уравнения этот закон выглядит следующим образом:
синус угла падения/синус угла отражения=nB/nA=показатель преломления среды B/показатель преломления среды А
Если вы посмотрите на чертеж, то заметите, что вертикально падающий луч, достигая границы сред, проходит, не преломляясь. Если же луч падает косо, он преломляется. Угол преломления изменяется быстрее, чем угол падения, в том случае, если луч переходит из оптически более плотной среды в менее плотную. В какой-то момент падающий луг попадает на границу сред (например, воды и воздуха) под таким углом, что его синус будет равен отношению nB/nА=1, в данном случае пв воздуха равно 1. Тогда и синус падения должен быть равен 1, а 1=sin 90°, то есть преломление в этом случае направлено параллельно границе сред. Если угол падения будет еще более пологим, выходящий луч отразится согласно закону: угол падения равен углу отражения.
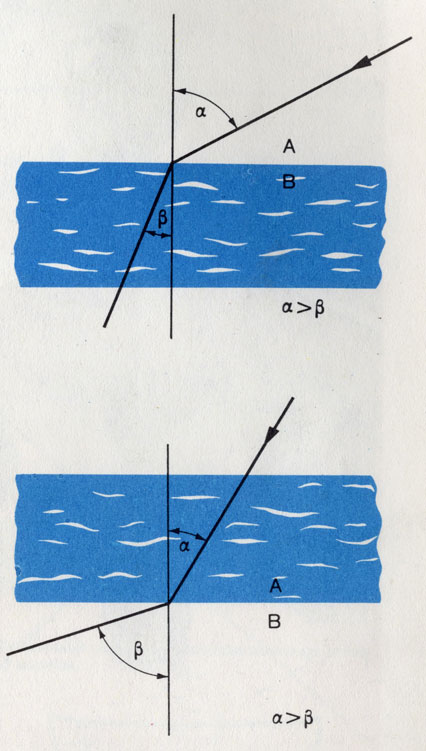
При переходе в оптически более плотную среду преломленный луч света отклоняется к вертикали, а при переходе из оптически более плотной в менее плотную среду - от вертикали
Мы столкнулись здесь с прекрасным примером того, как один закон оптики переходит в другой через граничное значение. Однако показатель преломления, кроме того, зависит от длины волны излучения. Дневной свет состоит из смеси волн разной длины - от фиолетовых до красных. Так как для каждой длины волны существует свой показатель преломления, «белый свет» на границе двух сред «разлагается», и мы видим цвета радуги.
Однако вернемся к нашему рыбаку. Луч его зрения, падая на поверхность воды, преломляется. Поэтому рыба вида гея удильщику совсем не там, где она находится в действительности, точно так же, как и его собственные ноги: они кажутся рыбаку «подломленными» у поверхности воды.
А теперь представим себя на месте рыбы. Ноги удильщика она видит непосредственно. Но если рыба находится на достаточном удалении (где и должна быть всякая осторожная рыба), то она видит еще и отражение ног от зеркальной поверхности воды.

Два зеркала поставлены под углом друг к другу. Углы между зеркалами представляют собой результат деления 360° на целые числа, то есть 120, 90, 60 и 45°. В зависимости от числа, на которое производится деление, мы видим кувшин 3, 4, 6 и 8 раз. Обратите внимание на то, что кувшин совершает в зеркале 'полный оборот'
Верхняя часть тела удильщика видна ей через границу поверхностей воды и воздуха. И тут, разумеется, справедливы физические законы (они ведь действуют независимо от того, знает о них рыба или нет!). Следовательно, луч зрения рыбы преломляется, так что она видит верхнюю часть туловища рыбака висящей в воздухе без ног. Говоря «видит», мы имеем в виду, что именно такое изображение возникает на сетчатке глаза. Процессов, происходящих при этом в мозгу, мы не касаемся. Нам вряд ли удастся проверить, что думает по этому поводу рыба, но что мы можем думать сами в подобных обстоятельствах, установить не составляет труда.

Принцип действия зеркального у глав калейдоскопе. Только 8 фишек на переднем плане 'истинные', все остальные фишки - их отражения в зеркальных углах
Не случайно в уже упомянутой книге (написанной Артуром Л. Фили) приводится доказательство того, что мы не всегда правильно судим о том, что видим «собственными глазами». Модный некогда цилиндр как нельзя лучше показывает, сколь легко мы можем ошибаться: наш рассудок просто не хочет «верить», что высота и ширина тульи этого головного убора одинаковы.

Оптический обман: высота тульи цилиндра равна ее ширине
Если пример с цилиндром покажется вам не очень убедительным, вспомните, как черное платье делает женщину стройнее, а подчеркнутая талия (как и сужение на тулье цилиндра) зрительно увеличивает ее рост.
ОБ ИСКАТЕЛЯХ СОКРОВИЩ
Однажды, будучи в Австралии, я увидел лавочку, где торговали снаряжением специально для искателей сокровищ. Это было в Сиднее, на маленькой улочке, огибающей небольшой парк.
В магазинчике продавались заступы, широкие лопаты, сита, ведра, молотки и прочие необходимые на этот случай предметы. Искателям приключений оставалось только, прихватив все это добро, отправиться в Австралийскую пустыню, чтобы рыть там шурфы в поисках золота, руды или драгоценных камней. Правда, прежде, как предупреждает висящее над прилавком объявление,будущие миллионеры должны обзавестись соответствующей лицензией на ведение разведки. (Такие лицензии выдаются желающим и по сей день.)
Чтобы искатели счастья точно знали, куда им надлежит держать путь и с чего именно начать, здесь же продаются карты и образцы пород и минералов. Истинные искатели сокровищ, очевидно, уже обзавелись всем необходимым, ибо, кроме меня, покупателей в магазине не было. Владелец продал мне за 25 центов образчик агата. К более крупным торговым операциям он, по-видимому, неособенно привык. Ведь серьезными поисками драгоценных минералов занимаются специалисты, а разработкой их месторождений - крупные концерны.

Два зеркала, составленные углом, показывают нам свечу троекратно
Но, чтобы ощутить себя в роли искателя подземных сокровищ, гражданину Германской Демократической Республики можно и не ездить в далекую Австралию. Прихватив средней величины молоток, он отправляется в Рудные горы в район Шенек - Клингенталь. На любой туристской карте обозначен Шнекенштейн. Добраться туда можно и пешком, и на машине - в зависимости от желания. В нескольких метрах возле шоссе среди деревьев возвышается скальный выход величиной с дом. Это Шнекенштейн - одно из немногих мест в Европе, где можно найти топазы. Чтобы и наши потомки могли еще увидеть кусочек интересного геологического ландшафта, скала объявлена заповедной. Проволочная сетка охраняет ее от молотков искателей топазов. Однако рядом с охраняемым участком находится большой каменный отвал, оставшийся от прежних разработок. Осторожно раскалывая молотком камни величиной с голову или с кулак, среди осколков можно обнаружить мелкие желтоватые кристаллы со стеклянным блеском. Чаще всего это кристаллы кварца, но среди них может попасться и топазик. После нескольких часов кропотливого труда счастливчикам случается стать обладателем полного спичечного коробка кристалликов. Только как отличить топаз от кварца?
Прежде всего по твердости. Топаз будет царапать кварц.
Австрийский минералог Фридрих Моос, современник Гёте, ювил в 1812 г. шкалу твердости минералов. Он выбрал довольно произвольно десять минералов и расположил их в ряд. Оказалось, что тальк, твердость которого была позже принята за 1, царапают все остальные минералы этого ряда. Алмаз способен сам царапать все минералы, а потому его твердость была принята за 10. Кварц по этой шкале имеет твердость 7, и его царапает топаз, твердость которого равна 8. Кристаллограф распознает эти минералы еще и по их принадлежности к различным кристаллографическим системам. Топаз обладает более низкой симметрией, чем кварц, так что эти минералы четко различаются и по форме кристаллов.

Так выглядит топаз в природной огранке, извлеченный из пустот в кварце
Сравнивая форму идеального природного кристалла топаза и искусственно ограненного, мы видим, что между их естественными гранями и искусственной огранкой нет никакой связи.
Драгоценные камни, как правило, обрабатываются без учета их кристаллографической ориентировки. Гранильщик преследует две главные цели. Во-первых, он стремится, чтобы камень по возможности сохранил свои размеры. Это и определяет выбор формы огранки. Во-вторых, ему хочется нанести предельное количество граней. Ведь чем больше граней, тем многократнее камень отражает свет и тем сильнее сверкает (вспомните о зеркальных углах!).
Возможно, у кого-то из читателей или их знакомых имеется великолепный золотистый топаз. Приобретая его, человек был уверен, что становится обладателем подлинного золотистого топаза. И его не обманули. Но в ювелирном деле золотистым топазом называется желтый кварц - цитрин.
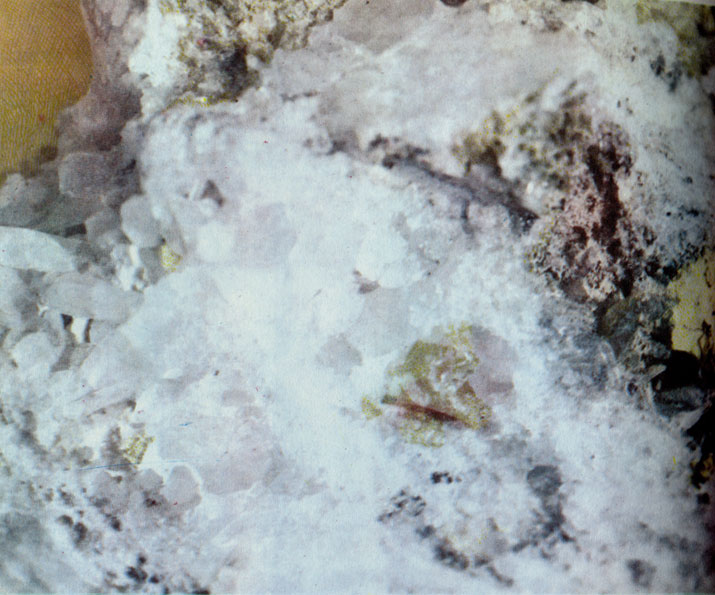
Кристаллы кварца и топаза из Шнекенштейна. Желтые включения - топаз
Из шкалы Мооса вы усвоили, да это и общеизвестно, что самым твердым из всех веществ является алмаз. Но как же тогда обрабатываются и шлифуются алмазы? И вообще - почему алмазы ценятся так высоко? На последний вопрос ответить трудно. Очевидно, человек особенно высоко ценит все то, что не поддается или с трудом поддается изменениям. В том числе и драгоценные металлы и камни. Древние греки назвали алмаз «адамас» - неодолимый, чем выразили свое особое отношение к этому камню. Конечно, у неограненных камней (алмазы тогда не гранили) наиболее очевидными свойствами были твердость и блеск. Алмазы отличаются высоким показателем преломления; 2,41 для красного цвета и 2,47 - для фиолетового (для сравнения достаточно сказать, что показатель преломления воды 1,33, а стекла в зависимости от сорта - от 1,5 до 1,75).

Кристаллографически топаз принадлежит ромбической сингонии
Белый свет составлен из цветов спектра. И когда его луч преломляется, каждый из составляющих цветных лучей отклоняется по-разному, он словно расщепляется на цвета радуги. Вот почему в алмазе мы наблюдаем «игру цветов». Кристаллографически алмаз относится к числу кубических кристаллов. От природы он наделен высокой симметрией и обычно образует октаэдрические кристаллы. Древних греков, несомненно, восхищало и это. Мало того, что камень исключителен по блеску и твердости, он имеет еще и форму одного из «совершенных» тел Платона! Ниже с помощью шариков для пинг-понга будет показано, чем объясняется эта исключительность.
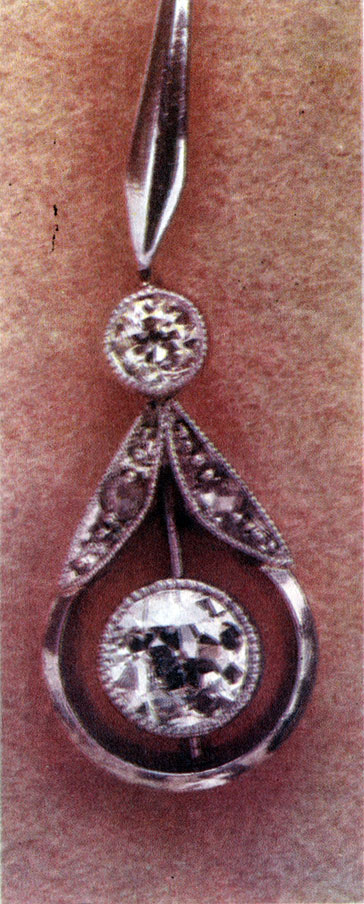
Ограненный камень ни одной своей гранью не напоминает природной формы кристалла
Еще и сейчас мы окружаем бриллианты и другие драгоценные камни ореолом необычайности. Всевозможные истории о «несчастных» камнях придают алмазам особую привлекательность даже в наш деловой век. На все, что связано с алмазами, набрасывается покров таинственности. Так, вместо того чтобы в числовом выражении охарактеризовать степень загрязнения алмаза включениями, о нем говорят: «Алмаз чистой воды». Равно как ни один ювелир не скажет: «Этот бриллиант весит 0,2 грамма», что было бы понятно везде и всем, а вынесет таинственный приговор: « Да здесь целый карат».

Два из крупнейших алмазов мира: 'Полярная звезда' (сверху)
При всем том разведка, огранка и сбыт бриллиантов лишены всякой романтики. Международный синдикат заботится о том, чтобы на биржи Лондона и Амстердама поступало ровно столько бриллиантов, сколько необходимо, чтобы цены на них оставались достаточно стабильными.

Два из крупнейших алмазов мира: 'Звезда Юга' (внизу)
Если алмаз предназначается для украшений, для него выбирается чаще всего бриллиантовая огранка. У октаэдра с помощью тончайшего металлического диска, края которого армированы алмазным порошком, снимаются две противолежащие вершины. Верхняя часть так называемого «дикштейна» (толстотаблитчатой заготовки) должна составлять 1/3, а нижняя - 2/3 общей высоты камня. После этого камень заливается легкоплавким металлическим сплавом с таким расчетом, чтобы одна часть его оставалась свободной. Сплав помогает удерживать камень при обработке. Затем камни шлифуются металлическими дисками, покрытыми алмазным порошком.

Бриллиант может насчитывать до 56 граней
Хороший бриллиант имеет 56 граней, из них 32 на верхней части и 24 - на нижней. Благодаря большому числу граней достигается многократное преломление света. Не все бриллианты бесцветны. Бывают окрашенные камни. Известен канареечно-желтый бриллиант Тиффани. Его вес - 128 карат (В начале 1981 г. в Якутии был найден желтый ювелирный алмаз весом 170 карат. Он был назван в честь XXVI съезда КПСС. - Прим. перев). Римский писатель и натуралист Плиний писал: «В каждом драгоценном камне как в капле воды отражено все величие природы».
ПОЛЯРИЗАЦИЯ
Электромагнитные волны, а следовательно и свет, могут быть описаны как поперечные колебания. В естественном свете все направления кажутся перпендикулярными лучу.
Поляризация при Отражении. Плоская стеклянная пластинка отражает часть света. При угле падения 56° (угол поляризации) отраженная часть света оказывается полностью поляризованной. Другая его часть проходит сквозь стеклянную пластинку и поляризуется частично.
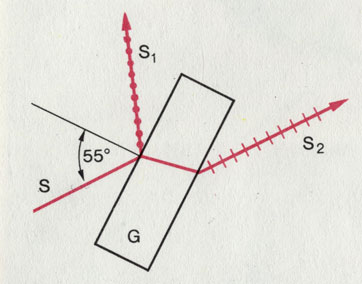
Поляризация при отражении
Поляризация в кристалле. Вследствие особенностей своего кристаллического строения так называемые двупреломляющие кристаллы, например известковый шпат, расщепляют световой луч в зависимости от его наклона к их кристаллографической оси на два луча с различными направлениями колебаний.
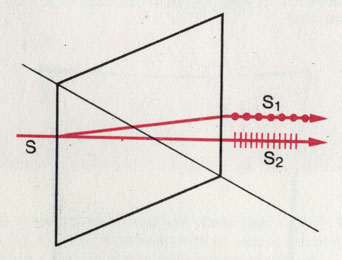
Поляризация в кристалле
Призма Николя. Для получения поляризованного света служат двупреломляющие кристаллы; два подобных кристалла приводятся в такое взаимное положение, что в месте их соприкосновения один поляризованный луч отражается наружу и тем самым гасится, тогда как другой распространяется прямолинейно.
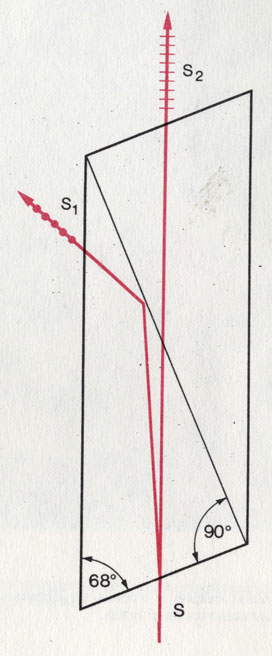
Призма Николя
Этот проходящий поляризованный луч служит далее для определения поляризации других веществ.
СУЕВЕРНЫ ЛИ ВЫ?
Разумеется, все мы не суеверны. Мы не верим ни гаданиям на кофейной гуще, ни картам, ни гороскопам. И вместе с тем нас радует случайно найденный четырехлистник клевера или цветок сирени с пятью лепестками. А всякий любитель карточной игры знает, что «счастливые» карты следует брать только по одной. В любой азартной игре бывает полоса везения и полоса неудач. Этому можно найти математическое объяснение.
Иногда мы читаем в романах, как какая-нибудь гадалка предрекает будущее, показывая кого-то или что-то в кристалле. Не станем говорить о достоверности такого прогноза. Нас больше интересует, каким образом делаются подобные трюки. В данном случае достаточно сумеречного освещения и некоторого расстояния между зрителем и таинственным объектом. Все остальное - вопрос техники.
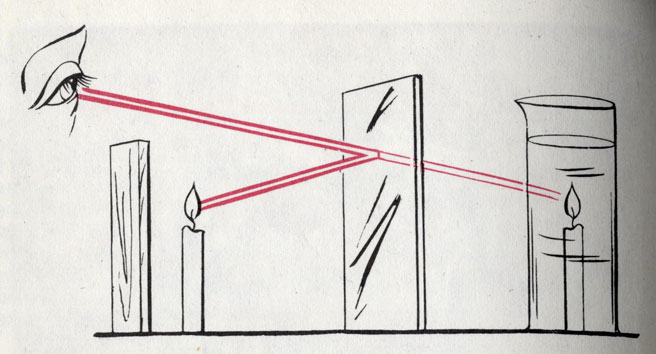
Полупрозрачное зеркало как по волшебству переносит свечу в стакан с водой
Хотите продемонстрировать кому-нибудь, как свеча горит под водой?
Пожалуйста. Поставьте свечу позади доски таким образом, чтобы зритель ее не видел, и отразите ее в его сторону с помощью стеклянной пластины. Зритель увидит смутное (а потому таинственное) зеркальное отражение. Если теперь позади стеклянной пластины поставить стакан с водой, выбрав такое расстояние, чтобы кажущееся изображение свечи совместилось со стаканом, то будет казаться, будто свеча в самом деле горит под водой! Конечно, этот элементарный фокус годится только для начинающих.

Обратите внимание на 'кафельный узор' бриллиантовой огранки
Обладая некоторым талантом и искусной техникой, можно заставить появиться или исчезнуть любой предмет. Стоит только нужным образом удалить его от зеркала. Секреты исполнения эффектных трюков обычно отличаются удивительной простотой.
Объяснить явления природы, как правило, много сложнее. Возьмем, к примеру, радугу. Тысячелетиями наблюдали люди появление на небосклоне сказочного полукруга. Его принимали и за мост, ведущий на небеса, и за доброе знамение, и за признак хорошей погоды. И только в 1631 г. французский философ, математик и физик Рене Декарт впервые дал научное объяснение этому явлению. (Вспомните: именно в это время люди начали все измерять!) Прежде всего Декарт установил, при каких условиях мы видим радугу.
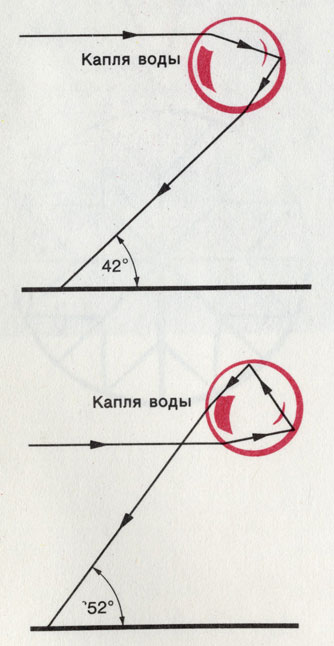
Так отражается и преломляется луч света в капле воды
Оказывается, только при низком положении солнца, когда оно находится над горизонтом не выше чем на 42° (то есть до полудня и на склоне дня), к тому же солнце должно быть за спиной наблюдателя. И наконец, в воздухе должны быть распылены мелкие капли воды от дождя или тумана. На равнине мы видим радугу как полукруг, а в горах (или с самолета) - как полный круг.
Это были общие рассуждения. Затем Декарт поставил опыт, который показал, что происходит, когда луч света падает на водяную каплю. Оказалось, что он отражается и преломляется согласно законам, незадолго до опытов Декарта открытым Снеллиусом.
Декарт сделал то, что отличает истинного естествоиспытателя. Он построил и рассчитал ход преломления и отражения 10 тысяч (!) падающих на каплю лучей. Лучи с номерами от 8500 до 8600 отклонялись на наибольший возможный угол, составивший 42°. За пределами этого угла радуги не бывает. Цвет дуги определяется зависимостью преломления от длины волны.
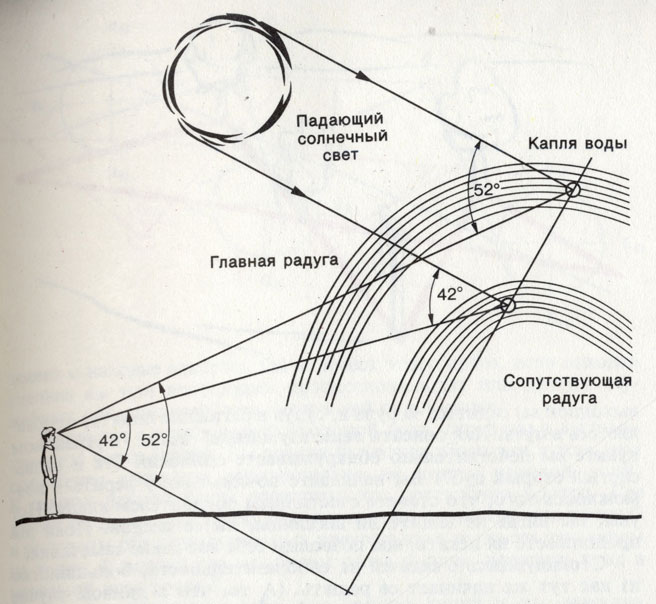
Столь поэтическое явление, как радуга, объясняется простыми физическими законами
Прославленный изобретатель Эдисон сказал однажды: «Гений - это один процент вдохновения и девяносто девять процентов труда». Декарт как нельзя лучше подтвердил этот афоризм: одна творческая идея и 10 тыс. скучнейших расчетов. Напрашивается вопрос: зачем Декарту понадобилось такое количество вычислений? На нашем рисунке изображены лишь два луча, и этого достаточно, чтобы все объяснить. Но мы потому и можем обойтись только ими, что вычисления Декарта были столь всеобъемлющими. Ему приходилось все время опасаться, что при каком-то угле падения выявится граничный случай, который поставит под сомнение всю теорию. Ведь всякая теория может считаться верной лишь тогда, когда она подходит для всех случаев, и может быть опровергнута, если отказывает в одном-единственном. Именно поэтому ученые так осторожны (или должны были бы быть осторожны!) в своих утверждениях. В науке на того, кто решается создать новую теорию, ложится груз необходимости доказать и обосновать ее. В таких случаях полезно вспоминать Декарта и Эдисона. Идея сама по себе не может служить доказательством. Один-два или десять опытов и расчетов уже доказательнее. Десять тысяч опытов или расчетов убеждают.
ПОИЩЕМ КЛАД
Произойти может многое. Другой вопрос, как велика вероятность того, что это случится именно с нами, встретится на нашем пути, в нашей жизни. Так ли уж, например, невероятно, роясь в лавочке букиниста, найти старинную географическую карту? Вам захотелось украсить этой картой свой кабинет. Вы приносите ее домой, начинаете рассматривать, радуетесь полустершимся рисункам на полях и вдруг... замечаете едва различимые старинные письмена: «Иди от виселицы к буку и считай шаги. Дойдя до бука, поверни на 90° влево и отсчитай такое же число шагов. Вслед за тем иди от виселицы к дубу, поверни еще раз вправо на 90° и пройди то же расстояние, что от виселицы до дуба. Ровно посередине линии, соединяющей обе найденные до того точки, я закопал большой клад, который теперь принадлежит тебе».
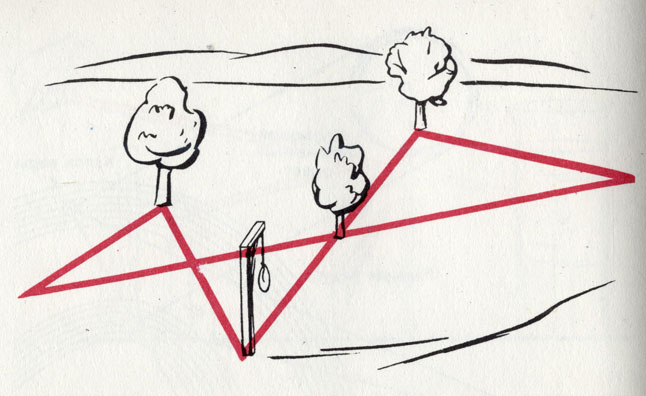
Представьте себе, что по этому эскизу вам надобно отыскать клад
Место при этом обозначено на карте крестом. Так как это не слишком далеко от вашего местожительства, в ближайший выходной вы садитесь за руль и, сунув в багажник лопату, отправляетесь в путь. Как описать ваше изумление, когда в указанном пункте вы действительно обнаруживаете одинокий бук и развесистый старый дуб?! Вы начинаете по-серьезному верить в возможность трго, что станете счастливым обладателем клада. Но, увы, вы нигде не видите ни виселицы, ни ее следов. Пока вы продолжаете их искать, мы позволим себе кое-какие замечания.
Столкнувшись с задачей на сообразительность, большинство из нас тут же начинает ее решать. (А то, что в данном случае предложена задача именно на сообразительность, вы, очевидно, уже сообразили.) Иначе поступит математик. Прежде чем тратить усилия на решение, он исследует корректность поставленной задачи. Сегодня и ученые, и инженеры все больше понимают значение такого подхода. Специалисты по научной организации труда указывают, что в исследованиях 80% всех неудач обусловлено плохо и неточно сформулированной задачей.
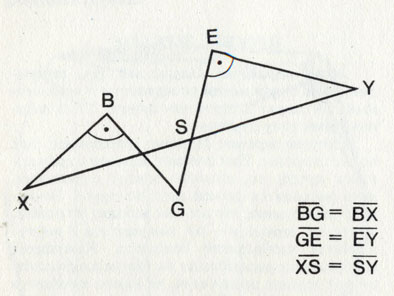
Так выглядит задача о поисках клада на языке математики
Но к нашему кладоискателю это открытие приходит слишком поздно. Он бродит с лопатой в руках и все еще ищет остатки виселицы. Наконец он встречает прохожего и начинает расспрашивать его. Прохожий задумался, огляделся вокруг и рассудил: «Зачем по тем временам надо было сооружать виселицу? Если уж тогда решали кого-то вздернуть, то делали это на суку».
Поразмыслив вслед за прохожим, кладоискатель решает попытать свое счастье, приняв, что виселицей служит бук. И вот он тщательно отмеряет шаги от бука (то есть виселицы) до дуба. Возле дуба он сворачивает направо и делает столько же шагов. Из этой точки он намечает линию к буку и мысленно делит расстояние пополам. Ну а потом, поплевав на руки, начинает копать большую яму.
Читатель между тем уже усомнился в том, что положение виселицы хоть как-то влияет на нашу историю. Но, возможно, его все же интересует, что произойдет, если там действительно зарыт клад.
Однако юристы об этом уже позаботились. В Гражданском кодексе ГДР (§ 361) написано:
«Монеты, предметы, имеющие культурно-историческое значение, или другие ценные предметы, которые были погребены столь долго, что их владелец не может быть более установлен, переходят с момента их находки в собственность народа.
Нашедший обязан предъявить находку компетентным государственным органам и подробно сообщить обстоятельства, при которых она была сделана. Он имеет право на положенное вознаграждение, если выполнил свою обязанность добровольно, заявив о находке властям. Он не имеет этого права, если находка сделана им при исполнении профессиональных или других служебных обязанностей, имеющих к ней отношение».
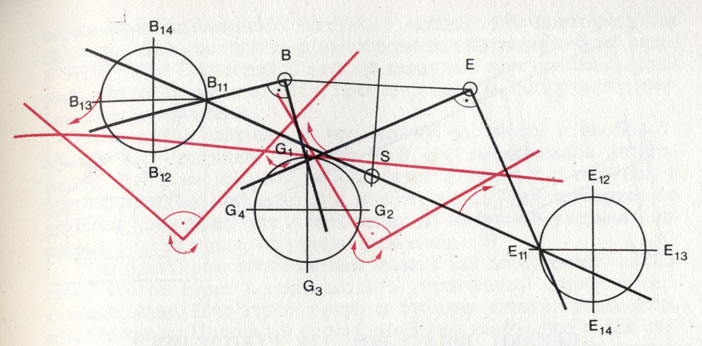
Та же задача о поисках клада, превращенная в технический чертеж шарнирного механизма
Покончив с юридической стороной дела, перейдем к математической части задачи. Вы хотели бы точно убедиться в том, что положение виселицы действительно не играет никакой роли. В рамках данной книги проверить это достаточно просто. Где лежит клад, мы уже знаем. Итак, наметим произвольную точку G и построим оба прямоугольных треугольника согласно указаниям на карте. И всякий раз мы будем снова и снова находить клад в знакомой нам точке S.
Теперь представим себе, что вместо линий у нас жесткие стержни. В точках В, Е и S они шарнирно закреплены, так что их можно вращать. В точках В1, G и Е1 благодаря особому устройству шарниров стержни можно смещать относительно друг друга.
Станем вращать точку G по часовой стрелке, наблюдая за сопряженными движениями точек В1, и E1. Вращаясь в ту же сторону, что и G, они тоже опишут окружности.
Когда G1 находится в верхней точке круга (на отметке 12 часов), соответствующие точки B1 Е1 располагаются в зеркальных позициях: B1 - на отметке 3 часа, E1 - на отметке 9 часов. Таким образом, точки В1 и Е1 смещены относительно G соответственно на +90 и -90°. Рычаг B1-S-E1 движется при этом всегда только вверх и вниз.
Увлекшись занимательной историей с кладом, мы изобрели шарнирный механизм, в котором два вращательных движения совершаются по кругам одинакового радиуса со сдвигом по фазе на +90 и - 90°. Подобные движения со сдвигом по фазе играют важную роль при создании механических распределительных устройств. Представим себе, что окружности - это вентили. В положении, отвечающем отметке 12 часов (0 часов), они закрыты. Затем мы немного открываем вентиль G от G1 до G2. Тогда вентиль В, до того слегка приоткрытый, откроется сильнее - от В11 до В12. А вентиль E, наоборот, закроется. При дальнейшем повороте G вентиль Е опять приоткроется, тогда как вентиль В будет установлен на малое пропускное отверстие. Конечно, могут быть построены и другие комбинации, смотря по тому, что требуется конструктору.
Как видите, от геометрической задачи на сообразительность мы незаметно перешли к шарнирным механизмам и к технике регулирования: красивый пример того, как многие, казалось бы, далекие друг от друга случаи из самых разных областей практической деятельности могут быть сведены к немногим математическим или физическим положениям.
ПЛОСКОЕ ЗЕРКАЛО
Закон отражения. Падающий луч, перпендикуляр к отражающей поверхности и отраженный луч лежат в одной плоскости. Угол падения равен углу отражения.
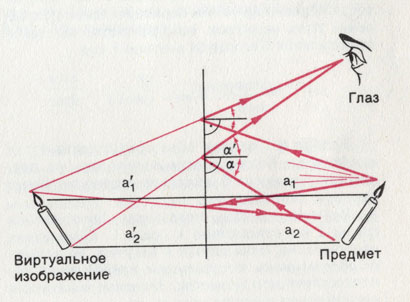
Плоское зеркало
Плоское зеркало. Предмет рассеивает свет во все стороны. Если плоское зеркало отражает пучок лучей, то, согласно закону отражения, лучи расходятся дальше друг от друга. Возникает впечатление, что все они исходят из одного места за зеркалом - от кажущегося ( виртуального) изображения предмета. Кажущееся изображение расположено на таком же расстоянии от зеркала позади него, на каком находится Действительное изображение перед зеркалом.
Зеркальная симметрия:
Закон отражения:
а'1=а1, а'2=а2.
Закон отражения:
α'=α
ПРЕЛОМЛЕНИЕ СВЕТА
Когда световой луч попадает на граничную поверхность двух разных прозрачных сред, например из воздуха на стекло, то часть света отражается, а часть проникает во вторую среду. Однако при этом первоначальное направление луча меняется: он преломляется. Закон преломления Снеллиуса выглядит как
sinα/sinβ=n(=const.)
Если β < α, то есть если преломленный луч отклоняется ближе к перпендикуляру, то преломляющая среда 2 является оптически более плотной, чем среда 1.
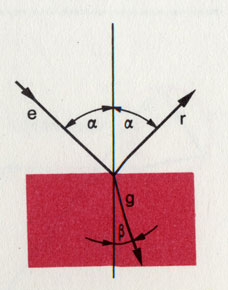
Преломление света
Величина n есть показатель преломления среды 2 по отношению к среде 1. Показатель преломления, отнесенный к вакууму, называется абсолютным показателем преломления соответствующего вещества. Значение показателя преломления зависит еще и от длины волны света.
| Вещество | Показатель преломления по отношению к вакууму |
| Вода | 1,3332 |
| Кронглас (в зависимости от сорта) | 1,5153-1,6152 |
| Флинтглас (в зависимости от сорта) | 1,6085-1,7575 |
| Алмаз | 2,42 |
| Воздух при нормальных условиях | 1,000292 |
ПОЛНОЕ ОТРАЖЕНИЕ
Когда свет переходит из оптически более плотной среды в менее плотную, преломленный луч отклоняется от перпендикуляра, так как β > α. Для этого случая
sinα/sinβ=n B / n A причем nB < nA
При больших углах падения α для того, чтобы произошло преломление, должно было бы соблюдаться условие sinβ>1 ; поскольку это невозможно, весь свет отражается и никакая его часть не испытывает преломления (полное отражение).
РЕНТГЕНОВСКИЕ ЛУЧИ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
Если пучок очень быстрых электронов наталкивается на металлический электрод, то свободные электроны вступают во взаимодействие с электронами металла. Электроны высоких энергий, проникающие внутрь атома, выбивают с одной из орбит его электронной оболочки электрон. На освободившееся место переходит электрон с другого, более высокого электронного уровня. При этом переходе высвобождается лучистая энергия в форме рентгеновского излучения. Оно имеет частоту порядка 1019Гц.
В рентгеновских вакуумированных трубках с помощью накаливаемого катода и прилагаемого высокого электрического напряжения создается электронный луч (пучок электронов), который затем бомбардирует металлический антикатод. В результате возникают рентгеновские лучи, которые легко проходят через стенки стеклянной трубки.
ПРЯЛКИ, ШКАТУЛКИ ДЛЯ РУКбДЕЛИЯ И КАРТИНЫ ХОГАРТА
Если мы внимательно рассмотрим изобретенный нами криво-шипно-шатунный механизм, то найдем, что его можно упростить. Движения точки G1 мы просто опустим, тем более что ведь G2 (виселица) может совпадать с одним из деревьев. Тогда в нашем приводе останутся только четыре элемента: неподвижный отрезок ЕВ, который в технике называют станиной; два подвижных отрезка, шарнирно закрепленных в станине, один из них называется кривошипом, другой - коромыслом (какой из отрезков считать кривошипом и какой коромыслом, зависит от определения), и, наконец, отрезок, шарнирно соединяющий концы кривошипа и коромысла (на подшипниках), который называется шатуном.
В простейшем случае, когда длина коромысла и кривошипа одинакова, мы имеем параллельный кривошипный механизм, или шарнирный параллелограмм. Он знаком нам по системе тяг и рычагов на колесах паровозов. Шатун с коромыслом и кривошипом можно соединить и таким образом, чтобы они описывали противоположно направленные, зеркально расположенные круги. При соответствующим образом подобранной длине коромысло будет совершать лишь качательные движения вперед-назад, в то время как кривошип станет двигаться по кругу. На этом принципе работают некоторые из первых изобретенных человеком машин, таких, как прялка и швейная машина с ножным приводом. В обоих случаях «коромысло» посылается ногой вниз. Вследствие этого начинает вращаться маховое колесо (кривошип). Его размах (или, как говорят в технике, маховой момент) должен быть достаточно велик, чтобы опять привести коромысло в исходное положение.
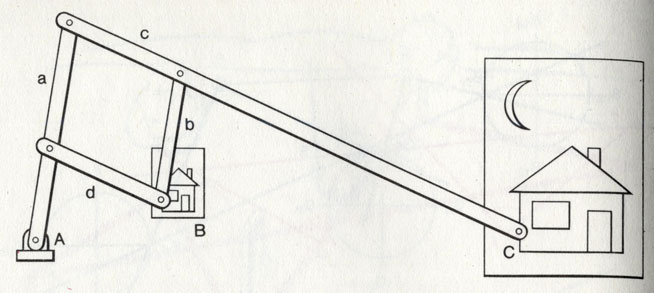
Пантограф - приспособление в виде шарнирного параллелограмма для перечерчивания чертежей в измененном масштабе
Вернемся еще раз к простому шарнирному параллелограмму. Шкатулка для рукоделия или инструментальный ящик помогут понять, как функционирует этот механизм.
Наверное, вы знакомы с чертежным прибором. В нем совместно действуют два параллельных кривошипно-шатунных привода, чем достигается параллельное перемещение линейки. Но интереснее всего, на мой взгляд, устройство пантографа - приспособления для копирования чертежей в измененном масштабе. В нем обошлись без неподвижного отрезка с двумя опорами, который заменен единственной неподвижной опорой (А), вынесенной за пределы шарнирного параллелограмма. Вторая «опора» (В) может свободно двигаться, в ней закреплен карандаш или штифт для обводки чертежа. При этом вся система выполняет соответствующие движения. Здесь используется тот геометрический факт, что существует точка, которая, будучи точкой пересечения удлиненного шатуна с линией АВ, повторяет все движения В, выполняя их в пропорционально увеличенном виде. В этой точке С находится второй карандаш или грифель, который, повторяя все движения, производимые В, вычерчивает увеличенное изображение.
Само собой разумеется, что можно поступать и наоборот: обводя в С оригинал, получать в В его уменьшенное изображение. Этот же принцип используется в системе с небольшой фрезой, которая помещается в положение С. Она гравирует по шаблону (находящемуся в положении В) надписи и рисунки одинакового начертания, но разных размеров.
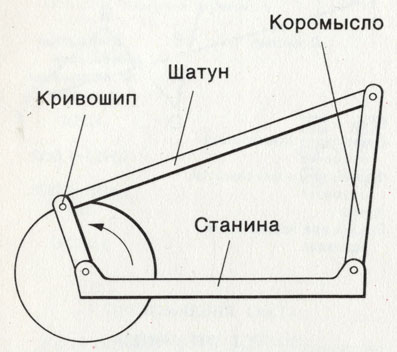
Кривошипно-коромысловый механизм, состоящий из неподвижной станины и подвижных коромысла и кривошипа, которые связаны между собой шатуном
При некотором воображении можно так перестроить пантограф, что он будет воспроизводить увеличенный шрифт в зеркальном виде. Для этого шатун и станину следует установить крест-накрест. Подобный способ особенно необходим в тех случаях, когда хотят получить отпечатки с оригинала. Ведь оттиск представляет собой зеркальное отражение изображения на печатной доске.
Широко известны жанровые картины английского художника Хогарта (1697-1764), изображающие сцены из жизни Англии XVIII в. С этих картин делались гравюры на меди. На печатной доске гравюра соответствовала картине, поэтому после печатания оттиск представлял собой ее зеркальное отражение. В данном случае граверу следовало бы воспользоваться пантографом.
Мы обязаны немецкому физику и мыслителю Г. X. Лихтенбергу (1742-1799) проникновенным описанием этих картин. Будучи физиком, Лихтенберг не преминул с помощью зеркал привести гравюры в согласие с теми картинами, которые послужили их оригиналами.
Мы уже знаем, что круговое движение кривошипа может иметь своим следствием качательное движение коромысла (и наоборот). С помощью надлежащих удлинителей шатуна и путем введения дополнительных элементов можно создать еще много других фигур. Причем важно, что существует также возможность преобразовать постоянную скорость вращения кривошипа в переменные движения, что сулит большие технические преимущества. Часто при обработке какого-либо изделия желательно перемещать его с постоянной скоростью, а после обработки возвращать тем же путем назад, но побыстрее. Кривошипно-шатун-ные передачи - один из возможных путей решения подобных задач, когда требуется изменить одновременно и направление, и скорость движения, оставив при этом в неприкосновенности направление, в котором действует приводной механизм системы.
ПОЭЗИЯ В ЗЕРКАЛЕ
Зеркальным отражением слов или фраз - игрой в слова - когда-нибудь занимались почти все. Но, пожалуй, не каждый знает, что так же играет и эхо, оно как бы возвращает нам зеркально отраженные слова. В школе нас учили, что волна это всегда волна. Неважно, будут ли это морские или звуковые волны, свет или рентгеновские лучи. Хотя длина этих волн различна, но физические законы, управляющие ими и подобные законам отражения или преломления, одинаково справедливы для всех видов волн.
Удовольствие, которое доставляет нам эхо, не зависит от возраста, его испытывают и стар и млад. В подходящих для этого местах люди кричат, поют, а то и пускают трели на тирольский лад. Какой длины слова или фразы способно возвращать нам эхо, зависит от расстояния между кричащим и отражающей стеной, которая, подобно оптическому зеркалу, должна быть непроницаемой и ровной (по отношению к длине волны). Такая стена не будет «глотать» волны, а станет отбрасывать их назад. Наконец, угол падения должен быть таким, чтобы отраженный звук не ушел невесть куда, а вернулся обратно к нам. Лишь в том случае, если все перечисленные условия выполнены, мы слышим эхо. Поэтому существует не так уж много мест, где мы воспринимаем его. Удивительно, что люди все-таки ухитряются находить такие места.
Однако есть еще одно условие: чтобы эхо было слышимым, звук должен возвращаться с достаточно большой задержкой во времени. Вспомните, как медленно приходится говорить оратору на больших митингах под открытым небом, дабы эхо не сделало его слова неразборчивыми.
Строители театров, концертных залов и кинотеатров стремятся погасить отражение звука от стен. Ив то же время частичное отражение должно происходить, в противном случае помещение будет акустически мертвым. Концертные залы, прославленные своей акустикой, обладают хорошо выверенным соотношением между подавленным эхом и резонансным колебанием стен.
Пословица гласит: «Как аукнется, так и откликнется» - но это не совсем справедливо. Эхо возвращает лишь столько слогов, сколько укладывается по времени в расстояние кричащий - стена - кричащий. Этим объясняются такие сокращения слов, как
«Ма-шут-ка» - «ут-ка», «но-во-сел» - «о-сел».
Для возникновения многократного эха необходимо несколько отражающих стен. Особый случай отражения представляют собой так называемые «уголки шепотов», которые подчас демонстрируют в старых церквях или замках. Разговор в определенной точке помещения слышен в одном или нескольких точно установленных местах. В простейшем случае строители используют отражательные свойства эллипса. Нередко в романах можно встретить истории о том, как такие уголки шепотов использовались для подслушивания всякого рода тайн. Однако скорее всего уголки шепотов отнюдь не плоды злого умысла зодчего, а следствие случайных особенностей конструкции.
Поэты тоже нередко занимаются игрой в отраженные слова и фразы. Известное стихотворение Христиана Моргенштерна (Христиан Моргенштерн (1871-1914) - немецкий поэт неоромантической школы. Его оригинальные стихи часто носили пародийный, иронический характер. Очертаниям некоторых из них автор придавал четкий геометрический рисунок. - Прим. перев) «Trichter» («Воронки») в оригинале выглядит так:
Zwei Trichter wandeln durch die Nacht. Durch ihres Rumpfs verengten Schacht flieBt weifies Mondlicht still und heiter auf ihren Waldweg u. s. w.
Моргенштерн мастерски использовал букву w в качестве концовки, замыкающей графический рисунок стихотворения. Ее форма, очерчивающая контур стиха, имеет вертикальную плоскость симметрии (обратите внимание на то, что это стихотворение о воронках и само имеет форму воронки, а буква w напоминает две составленные воронки). [В русском алфавите буква w отсутствует, но переводчики попытались передать эту стихотворную шутку, по. возможности сохранив внешний облик стихотворения:
Воронок пара шла сквозь лес. Сквозь шахты суженных телес тек белый лунный свет беззвучно, ясно в люки талий на путь их через лес и да ле е. - Перев.]
В очертаниях этого стихотворения Моргенштерн сознательно следует старинной типографской традиции. В XVI в. в книгах было принято симметричное оформление титульного листа. Слова при этом произвольно разрывались согласно задуманному, расположению строк; остаток слова в угоду симметрии мог перейти даже на следующую страницу, где набирался уже обычным, мелким шрифтом. Но истинное искусство симметричного «отражения» слов началось с составления целых фраз, которые можно было читать слева направо и справа налево. Отдельные слова, такие, как Отто, Анна или Тит, казак, шалаш, подобрать нетрудно. Сложнее придумать комбинации: «топор - ропот», «дороден -недород». Далее при игре во фразы-перевертыши надо усвоить, что при «зеркальном чтении» слова делятся на слоги иначе, чем при прямом: «Изредка так дерзи». При чтении этой фразы наоборот из «дерзи» и «ка» (взятого уже от «так») получается «изредка». Такие фразы существуют во всех языках. Вот, например, немецкая " Ein Esel lese nie" («Осел не читает никогда»), составленная К. Фридрихом из Зейферсдорфа, или русские «И пикантен и нет накипи», «А ремень не мера», «Кинь лед зебре, бобер, бездельник», «А ругала баба балагура». Для образования подобных фраз полезно сначала составить маленький словарь-перевертышей.
В заключение заметим, что существуют и «рассказы-перевертыши», в которых отражаются не буквы, а слова. Одна история (переведенная с английского) начинается словами «Джонс годами разрабатывал теорию времени», а кончается так: «Времени теория разрабатывала годами Джонса». Между этими фразами заключена довольно фривольная история, которую можно читать в обе стороны: с начала до конца и с конца до начала.
Совсем другой вопрос: имеют ли такие истории смысл или просто их авторы не нашли лучшего применения своему остроумию и трудолюбию? Но если кто-то целый рабочий день, а то и дольше размышляет только «о серьезных вещах», уже наверное, он имеет право отвлечься на такую «безделицу». Кстати, если вы где-то прочтете "Kauten Sie jede Woche vier gute bequeme Pelze xy" («Покупайте каждую неделю четыре прекрасные удобные шубы ху»), не подумайте, что и здесь скрыто какое-то отражение, - это просто пробная фраза телетайпной связи. Она содержит все буквы латинского алфавита, а некоторые, такие, как буква «е», - даже по нескольку раз. Те, кто работает с телетайпом, таким образом контролируют правильность передачи всех букв.
И наконец само зеркало играет в поэзии большую роль прежде всего благодаря многозначности и символичности этого предмета. Иногда зеркало выражает идею самопознания и самокритики. Вспомните хотя бы Тиля Уленшпигеля (ведь само его имя Ойлен-Шпигель и означает «Зеркало Совы»). Или вспомните знаменитый роман Джозефа Конрада «Зеркало морей».
Детективная литература тоже не обходится без зеркала и зеркального шрифта. Не так давно появился детектив Э. Гарднера «Моль в норке». Герой его, Перри Мэзон, находит в комнате два призыва о помощи, написанные губной помадой. В одном случае мольба открыто начерчена на зеркале, а в другом - снизу на крышке стола. Очевидно, что истинным может быть лишь один из призывов, но какой? Полицейский справедливо полагает, что истинный призыв должен быть спрятан, иначе гангстеры уничтожили бы надпись. Однако он склонен все проверять на деле и поручает помощнику повторить действия жертвы, еще раз написав призыв на нижней стороне крышки стола. Чтобы «враг» не заметил, пишущий должен спокойно сидеть за столом и не глядя, вслепую писать снизу на его крышке.
Умудренные опытом любители детективов уже сообразили, наверное, как будет выглядеть эта надпись под столом. При таком способе письма шрифт на нижней стороне крышки стола мог получиться только зеркальным. Однако в романе говорится, что фраза написана правильно: слева направо. А это значит, что доска стола была предварительно перевернута. Отсюда и закручивается сюжет. Если бы так же просто обнаруживались действия преступников и в реальной жизни!
В одном из журналов «Немецкое уличное движение» за 1962 г. появилось сообщение, что в Англии, в городе Кенте, надпись на машинах скорой помощи пишется дважды: один раз обычным образом, а второй - зеркальным шрифтом. Благодаря этому водители движущихся впереди машин легче узнают такую машину в зеркале заднего вида и уступают ей дорогу. Возможно, это - правдоподобное сообщение, хотя оно было напечатано в апрельском номере журнала.
«МОРДНИЛАП»
Знаете ли вы, что такое «морднилап»? Если нет, то не ищите это слово ни в энциклопедии, ни в словаре иностранных слов. Там его не сыщешь. Но это еще вовсе не доказывает, что оно вообще не существует. Так, раньше в словаре не было и слова «нособом». И только, когда поэт Христиан Моргенштерн написал из чистого озорства и жизнелюбия:
Его еще нету в Брэме И в Майере тоже нет, Его не найдешь в Брокгаузе...
посвятив этому самому нособому целое стихотворение, в Энциклопедии Брокгауза появилась соответствующая статья: Нособом - сказочный зверь, который бегает на своем носу, придуманный Христианом Моргенштерном в одном из стихотворений сборника «Песни висельника».
Но слова «морднилап» пока еще не найти нигде в отличие от его зеркального отражения, которое читается «палиндром». Палиндромы - это буквы, слова, фразы или цифры, которые могут читаться и слева направо, и справа налево. О словах и фразах мы уже говорили, с числами обстоит точно так же, как и с буквами или словами. А отражается как А. Точно так же 8 вновь прочитывается в зеркале как 8. О остается 0. Прочие цифры лишены плоскостей симметрии - они появляются в зеркале «наоборот».
Палиндромные числа сохраняют свое значение, с какой стороны их ни читай. Простейший случай, вероятно, представляет собой число 11. Год 1881 обратим. Ближайшая обратимая дата - 1991 год. Пусть он будет годом палиндромов для тех, кто увлекается проблемами отражения.
Подчас встречаются числа-палиндромы с весьма необычными свойствами. Например, мастера показывать числовые фокусы исходят из числа 999 999, то есть миллион минус единица. Если разделить его на 7, то получится
999999:7 = 142857,
число, по виду ничем не примечательное. Его особые свойства раскрываются только при умножении:
142 857 • 2 = 285714,
142 857 • 3 = 428571,
142 857 • 4 = 571428,
142 857 • 5 = 714285,
142 857 • 6 = 857142.
Все произведения состоят из тех же шести цифр. Если в любом из этих чисел начать с 1, то дальше всегда следует 4, потом 2 и т. д. Нужно только после конечной цифры числа вернуться к его началу и продолжать читать с первой цифры. Последовательность цифр постоянна: 142 857. Любители подобных фокусов могут, конечно, развить этот ряд чисел далее. При желании можно прибавлять соответствующие числа, всегда получая при этом одну и ту же последовательность цифр, пока в конце концов снова не появится зеркальное число - 999 999.
Другая шуточная задача с палиндромами явствует из следующих рядов:
123 456 789 • 1 • 9 = 111111111,
123 456 789 • 1 • 9 = 222222222
и т. д. вплоть до
123 456 789 • 9 • 9 = 999999999.
Исследован также вопрос о том, существует ли взаимосвязь между простыми числами и палиндромами. Канадец Н. Гриджмен установил, что простые числа с нечетным числом цифр образуют определенные группы. Вот некоторые из них:
181 373 12721,
191 383 12821.
Однако в математике морднилап, кажется, еще менее необходим, чем в языке. В то же время математика не раз вдохновляла иные поэтически настроенные души на литературные излияния. Так, один английский статистик (!) по фамилии Юден создал около века назад хвалебный гимн кривой Гаусса. Он писал (в форме такого рода кривой): «Закон нормального распределения ошибок выступает в опыте человечества как одно из самых широких обобщений натуральной философии. Он служит ведущим инструментом исследования как в физике и социальных науках, так и в медицине, сельском хозяйстве или технике. Он является незаменимым орудием для анализа и обработки данных, полученных из наблюдения и эксперимента».
Математик Карл Фридрих Гаусс, о котором мы уже упоминали, когда говорили об измерении больших треугольников, разработал форму кривой, столь воодушевившую Юдена. Если выполнить большое число измерений какого-либо отрезка - длиной, скажем, в 1 м, - то лишь очень немногие из измерений окажутся равными в точности 1,00 м. Многие измерения дадут значения 0,981 или 1,01 м. Если теперь нанести на диаграмму частоту появления каждого значения измеренной величины, то в идеальном случае получится кривая Гаусса. Подобные кривые можно получить, скажем, при измерении бобов или горошин.

В старину симметрию в формировании книг соблюдали даже в ущерб правописанию
Пока кривая нормального распределения выглядит симметрично, речь идет о случайных отклонениях. Но всякое значительное отступление от симметрии свидетельствует о необходимости установить его причину. В простейшем случае неточным может оказаться измерительный инструмент. Хуже, когда не внушает доверия лаборант, производящий измерения. Однако причина может также заключаться в том, что в число горошин попали (случайно или намеренно) представители иного сорта, которые подчиняются распределению с другими параметрами.
Подобные сведения - и не только подобные - может почерпнуть статистик из нормального распределения. Всем нам есть чему поучиться у Гаусса. Как известно, при планировании и подведении итогов мы часто оперируем средними значениями. Средний годовой доход граждан составляет столько-то. Средний размер обуви мужской части населения такой-то. Среднее потребление пива такое-то и т. д. Однако такое среднее значение еще далеко не отражает истинного положения. Людям с особенно маленькими или особенно большими ногами известна даже песенка на эту тему. А что касается пива, то грудные младенцы, хотя и являются гражданами страны, его не потребляют. Получается, что отцы должны пить за двоих, троих, а то и четверых, чтобы поддержать средний уровень на душу населения. Поэтому Юден с полным правом написал, что нормальное распределение «является незаменимым орудием для анализа и обработки данных». К непроанализированным средним значениям следует питать глубокое недоверие.
Давайте прикинем, какими средствами в среднем располагают американские миллионер и нищий. Ну, в простейшем случае миллионер обладает как минимум 1 млн. долларов, а нищий - О долларов. Легко вычислить среднее значение:
В старину симметрию в оформлении книг соблюдали даже в ущерб правописанию.
1 000 000 + 0/2 = 500000 долл.
Следовательно, средний американец должен был бы иметь 500 тыс. долларов. В чем тут ошибка?
Расчеты средних величин годятся лишь для больших чисел! Значит, 1000 миллионеров и 1000 нищих? Но и в этом случае вычисление не даст правильного результата:
1 000 000 - 1000 + 0 • 1000/2000 = 500000 долл.
Действительная ошибка заключается в том, что нищие и миллионеры располагаются на противоположных концах кривой распределения имущественного состояния народа. Между ними находятся 150 млн. человек, владеющих 10, 100 или 1000 долларами. И средняя величина или среднее значение лишь в том случае приобретает смысл, когда кривая нормального распределения учитывает все имущественные состояния. Не подлежит сомнению, что наблюдения над распределением состояний всех граждан США покажут, что такое распределение не является нормальным. Тут-то именно следует приняться за математический, экономический и политический анализ.
ЛОГИЧЕСКИЕ ОШИБКИ С СИММЕТРИЙНОЙ ПОДОПЛЕКОЙ
| Стороны | А | В | С |
| Верхняя сторона | красный | красный | белый |
| Нижняя сторона | красный | белый | белый |
Решая математические задачи, имеющие (действительное или кажущееся) «симметрическое решение», мы быстро приходим к ответу. Примером такого рода задач может служить равномерное распределение разности между двумя величинами (то есть к каждой величине требуется прибавить половину этой разности).
Возьмем три одинаковых куска картона А, В и С. Закрасим А с двух сторон в красный цвет, С - в белый и В - с одной стороны в красный, а с другой в белый:
Теперь бросим все три картонки в мешок и вытащим одну из них. Не глядя на ее обратную сторону, положим картонку на стол. Допустим, перед нами красная поверхность. Так как один из кусков, С, выкрашен с обеих сторон в белый цвет, то мы видим либо кусок А (красный - красный), либо кусок В (белый- красный) красной стороной кверху.
И только тут возникает сама задача: как велика вероятность того, что, подняв лежащую перед вами картонку, вы увидите красную обратную сторону? Иными словами, какова вероятность того, что это картонка А1 Вам, конечно, нет надобности долго раздумывать: раз речь идет о двух кусках картона, из которых один А, а другой не А, то решением (симметрическим) будет, разумеется, 1:1, или 50% к 50%. Но, к сожалению, наше «разумеется» ошибочно. Две картонки, между которыми надлежит сделать выбор, имеют следующие красные стороны:
картонка А - верхнюю,
картонка А -нижнюю,
картонка В - верхнюю (снизу она белая).
Одна из сторон обращена кверху с вероятностью 33,3%. Для картонки А эта вероятность, однако, удваивается (верхняя и нижняя стороны), а для картонки В - нет. Следовательно, с вероятностью 66,6% на столе лежит кусок А. Как видим, на основе этого рассуждения можно заключить выигрышное пари: ответ 1:1 столь импонирует большинству людей, что мысль о возможности другого решения им даже не приходит в голову.
Аналогичным образом построена задача о двух детях. Некто говорит: у меня двое детей. По крайней мере один из них - мальчик. Значит, другой - либо мальчик, либо девочка. Какова вероятность того, что второй ребенок - мальчик? Соображаем: в среднем девочек столько же, сколько и мальчиков. Следовательно, сразу же напрашивается ответ: вероятность будет равна 50%. Мы столь быстро склоняемся к такому ответу в силу его симметричности.
Однако правильный ответ мы получим, продумав все возможные комбинации в семье с двумя детьми.
Один ребенок всегда старше, другой моложе. Значит, возможны случаи ДСММ, МСДМ, МСММ, но невозможна комбинация Дс Дм, так как один ребенок является мальчиком по условию задачи. Среди трех возможных случаев лишь в одном второй ребенок - тоже сын, и соответственно вероятность этого составляет 33%. В 66% случаев второй ребенок будет девочкой, если только первый - определенно мальчик.

Математик Юден посвятил кривой Гаусса хвалебный гимн, придав тексту гимна форму такой кривой
Еще затруднительнее следующий вопрос: вы ищете величину А, заключенную между 90 и 110. Ее значение вам неизвестно. Требуется определить число, для которого ошибка в обе стороны будет минимальной (то есть симметричной). Вам, конечно, хотелось бы назвать число 100, так как оно находится посередине между 90 и ПО, но вы не доверяете себе, ибо есть основания полагать, что эта величина неверна (такое решение кажется слишком простым). Чтобы вычислить правильное значение, воспользуемся условием: ошибка сверху и снизу должна быть одинакова. Значит,
х-90/90 = 110-х/110
(х-90)110-(110-х)90,
110х - 9900 = 9900 - 90x + 90x + 9900,
200x = 19 800,
x=99
От 90 до 99 ошибка составляет 10%, и 11 от 110 тоже отвечает 10%-ной ошибке. Неожиданность полученного результата вытекает и из определения понятия «ошибка», и из нашей склонности обращаться к симметричным значениям.
«ТЫ ДОЛЖЕН ЦЕЛИКОМ ОТДАТЬ СЕБЯ ИСКУССТВУ!»
Это требование, естественно, выдвинуто не вполне всерьез. Пожалуй, лишь очень немногие действительно беззаветно отдаются искусству (любому его виду). Непременной предпосылкой к тому является профессиональное мастерство в музыке, литературе, живописи или какой-либо иной сфере искусства, далеко превосходящее уровень таланта. А если гений, отдаваясь своему искусству, способен еще и одерживать успехи на поприще экономики, то это означает, что он посвятил себя не только искусству. (Это не столько упрек, сколько констатация факта.)
Фраза об искусстве, которому ты должен себя целиком посвятить, - и слова, и музыка, на которую они положены, - принадлежит Йозефу Гайдну. Для нас этот его канон интересен с точки зрения симметрии. Это место из Гайдна, как и другие примеры, касающиеся симметрии в музыке, мне сообщил Йохен Глезер.
В теории музыки (основах композиции) известны различные симметрические формы. Простейший случай - обращение интервала. Оно исходит из звуковой последовательности (то есть мелодии), которая испытывает зеркальное отражение в плоскости, параллельной средней линии нотного стана, так что направления музыкальных интервалов изменяются на обратные. Если мелодия (звуковой ряд) оригинала повышается, то в обращении она понижается на такой же интервал, и наоборот. Искусство композиции состоит в том, чтобы с помощью этого формального изменения направления создать осмысленную мелодию, которая прослушивалась бы еще и в обращенном виде.

Музыкальные отражения. a - пример музыкального обращения интервалов, зеркальная плоскость параллельна нотной линейке; б - так строится ракоходное отражение: в - так строится ракоходное отражение с обращением; г - канон Гайдна, в котором встречаются все формы отражений в музыке. Кроме того, его можно петь в прямом и обратном направлении
Вольфганг Амадей Моцарт сочинил свою знаменитую фортепианную сонату ля-мажор с вариациями на одну музыкальную тему. Это не давало покоя композитору Максу Регеру, который придумал еще 8 вариаций на ту же тему, и среди них одну в обращенной форме.
Другой вариант зеркального отражения в музыке более понятен для немузыканта. В этом случае зеркальная плоскость ориентирована перпендикулярно к нотным линейкам. Отраженные ноты кажутся такими, какими они действительно выглядели бы в зеркале. Начиная от зеркальной плоскости оригинал проигрывается в обратном направлении. Такое зеркальное нотное письмо носит название «ракоходное», по ассоциации с обыкновением раков пятиться назад.
Опытные музыканты способны еще к тому же обратить и ракоходную часть пьесы. При этом в зеркальной части снова меняется направленность звукового ряда по высоте. Понижающаяся мелодия ракоходной части становится повышающейся, и наоборот. Человек, не столь искушенный в музыке, едва ли еще сможет распознать, как связан с оригиналом дважды по-разному отраженный мотив.
И наконец, бывает еще и зеркальный вариант ракоходного отражения, когда нотный лист тоже как бы ставится на голову, - и в таком виде эту музыку поют или играют. (А какая экономия бумаги!)
Так вот, Йозеф Гайдн в своем каноне применяет различные способы отражения основной мелодии: ракоходное отражение, ракоходное отражение с обращением интервала и зеркальное ракоходное отражение. Самое удивительное, что в результате мы слышим не кошачий концерт, а (как всегда у Гайдна) благозвучную мелодию.
Как-то в телевизионной передаче я наблюдал за двумя участниками, бегло говорившими в обратном направлении. Собственно, это распространенный среди школьников тайный язык (На Руси таким языком-перевертышем пользовались офени - торговцы вразнос - и бурсаки. - Прим. перев), когда «оволс аз оволс» перевертывается задом наперед. Но в данном случае привлекало внимание то, что мелодия исполнялась «в правильном направлении», а весь текст о «малышке Гансике» - в зеркальном. О такой возможности не подумал даже Гайдн. Если бы в его распоряжении находились шесть таких телезвезд, то он мог бы поручить им повторно пропеть каждую из шести его мелодий с зеркальным произнесением текста. Тем самым он задал бы работу 12 певцам, из них 11 воспроизводили бы либо текст, либо мелодию в зеркальном отражении.
ОПЕРАЦИИ СИММЕТРИИ (СИММЕТРИЧЕСКОГО ПРЕОБРАЗОВАНИЯ) В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
1. Вращение вокруг оси. Возможны повороты только на 60, 90, 120 и 180°.
2. Отражение в зеркальной плоскости.
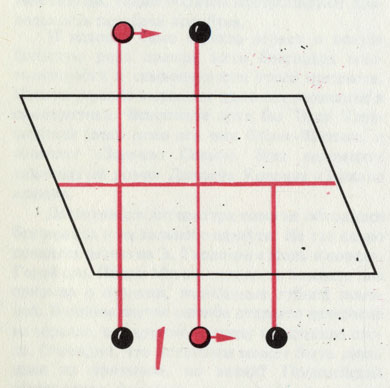
Операции симметрии
3. Совместное вращение и отражение.
4. Скользящее отражение. При этом узел решетки испытывает одновременно отражение и некоторое смещение.
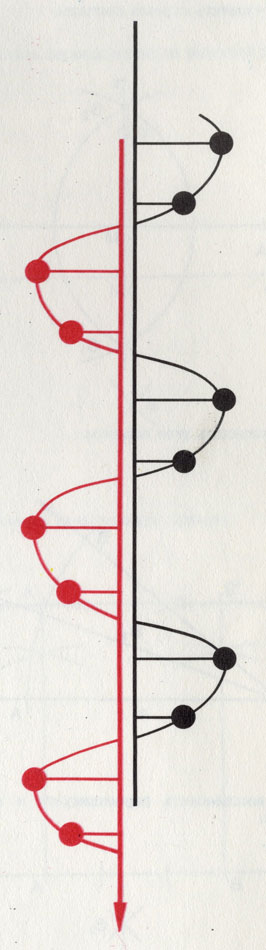
Операции симметрии
5. Винтовые оси обусловливают поворот на 60, 90, 120 или 180° и одновременно смещение (трансляцию) узла решётки вдоль оси вращения. Возможны левые и правые винтовые оси.
ЧЕМ МЕДЛЕННЕЕ, ТЕМ БОЛЬШЕ
Наша шкала (абсолютных) температур носит имя английского физика лорда Кельвина (1824-1907). Прежде чем стать бароном, он был просто Уильямом Томсоном. Томсон, лорд Кельвин, выполнил основополагающие исследования в области термодинамики и учения об электричестве. Однако нас интересуют рассуждения Томсона о возникновении кристаллов. Ведь кристаллы не просто существуют от века в неизменном виде. Они должны зарождаться и расти. Томсон продумал вопрос о том, где и как образуются кристаллы, и установил, что они развиваются путем осаждения из растворов. Сахар в виде крупных кристаллов - так называемый кандийский сахар - кристаллизуется из водных растворов, графит - из жидкого железного расплава. Кристаллы льда - при замерзании воды.
Бывают и твердые жидкости (вспомните о стекле). Из твердых растворов тоже могут возникать кристаллы. Однако они образуются не только из растворов, но и из газов или паров при непосредственном переходе вещества из газообразного состояния в твердое. В таких случаях говорят о сублимации, или возгонке. Из прозрачного зимнего воздуха выпадает кристаллический иней, оседающий на кустах и деревьях. Стекла автомобилей за ночь покрываются льдом, хотя никаких признаков появления жидкости перед тем не наблюдалось.
В какой-то момент, рассуждал Томсон, несколько атомов или молекул должны как-то соединиться воедино, чтобы образовать по крайней мере одну элементарную ячейку будущего кристалла. И тут последовала типично научная постановка вопроса: какова вероятность образования подобной ячейки, кристаллического зародыша, крохотного кристаллика?
Когда речь идет о величинах атомного или молекулярного порядка, в большинстве случаев не имеет смысла говорить о каком-то определенном событии. Осмысленным является лишь вопрос о вероятности этого события. Затмение Луны наступает с точностью до секунды и может быть предсказано за 1000 лет вперед. Но вот столкнутся ли между собой гдве молекулы газа - об этом можно судить только в вероятностной форме.
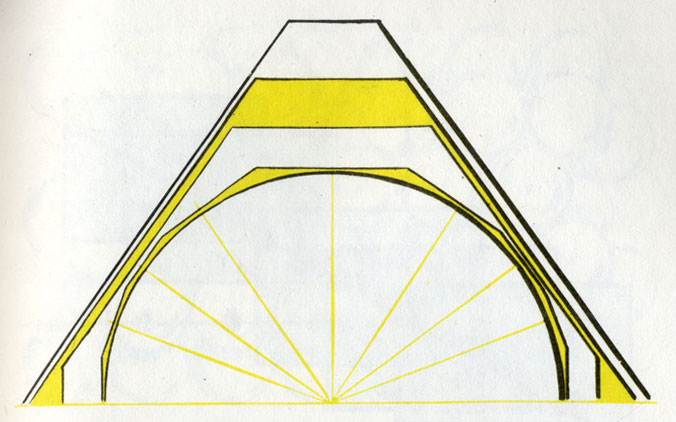
Верхняя грань (001) растет быстрее всех других граней. Вследствие этого она становится все меньше и в конце концов исчезнет совсем
Весьма типичен и способ, с помощью которого Томсон решил поставленную проблему. Он обратил внимание на то, что и вода, и снег способны улетучиваться. Значит, они обладают определенным давлением паров. Если это давление достаточно велико по сравнению с внешним давлением в окружающей среде, то вода или снег испаряются. По мере того как масса воды уменьшается и наконец становится столь малой, что образуется капля, все большую роль начинает играть ее поверхность. Томсону удалось показать, что при весьма малых диаметрах капелек давление пара возрастает необычайно резко. Отсюда всякая маленькая капля или кристалл становятся крайне неустойчивыми, и вероятность их «выживания» (сохранения) очень низка. В сущности, образование кристалла при таких условиях становится вообще невозможным. К счастью, однако, природа располагает средством обходить закон Томсона. Оказывается, при образовании капелек на всех неровностях, углах и прочих выступах отлагаются мелкие кристаллические зародыши, которые увеличивают диаметр капельки. Благодаря этому давление пара в капельке понижается и устойчивость ее возрастает. Не случайно слабый иней прежде всего оседает на тонких ветках и проводах, а лужи всегда замерзают с краев (у неровных выступов).
Кстати, когда при восточном ветре выпадает иней, в какую сторону бывают направлены ледяные кристаллики? Те, кто не родился в горах, склонны представлять себе форму растущих кристаллов обтекаемой: дескать, зародыш возникает под защитой ветви и растет по ветру. Неверно! Зародыши образуются на наветренной стороне, и иней растет против ветра, или, лучше сказать, навстречу «привнесу материала», который обеспечивается ветром. Взаимоотношения при образовании зародышей мы можем наблюдать также в нашем домашнем обиходе. Интересно, что тут есть наблюдения, любопытные и для мужчин, и для женщин.
Первое наблюдение - для представительниц женского пола. При варке фруктов или овощей на поверхности воды непосредственно перед закипанием образуется пена, в которой собираются все сорные частицы. Хорошая хозяйка в этот момент - пока еще не началось бурление - снимает пену шумовкой. Что тут произошло?
Вода в некоторых местах нагрелась до температуры кипения. Образовались мельчайшие пузырьки, сами по себе неустойчивые. Чтобы увеличить свой радиус и тем самым повысить вероятность собственного сохранения, они прицепляются к частицам сора. Благодаря этому пузырьки могут расти и вместе с мусором поднимаются кверху. Этим примером я обязан моей жене. Но и поварам-мужчинам, несомненно, знакомы такие наблюдения.
Теперь обратимся к эксперименту для мужчин (но да будет замечено, что и женщинам отнюдь не возбраняется его провести). Нальем в стакан напиток, содержащий углекислоту. Смотря по степени жажды (в том числе и жажды знаний), это может быть газированная вода, пепси-кола, пиво или шампанское. Подождем, пока исчезнет пена и жидкость перестанет пузыриться. Если теперь опустить в напиток ложку или соломинку, пузырьки тут же начнут образовываться снова.
Обратимся теперь к росту кристаллов. Но прежде нам придется еще раз вернуться к Платоновым телам. Мы уже однажды установили, что все они принадлежат кубическим классам симметрии. Открытым остался вопрос о том, как возникают отдельные грани. Представьте себе мысленно куб, или гексаэдр, как говорил Платон. Потом возьмите (тоже мысленно) острый нож и обрежьте все восемь его вершин. На кубе появятся треугольные грани. Будем увеличивать их размеры, последовательно отрезая новые параллельные плоские ломтики. Соответственно площадь прежних граней будет становиться все меньше и меньше, пока наконец совсем не исчезнет. Куб превратится в октаэдр. Можно провести и обратный эксперимент - снова сделать из октаэдра куб, мысленно уменьшая площади треугольных граней. Очевидно, что на любой стадии такого преобразования плоскости симметрии сохраняют свое положение.
Рассмотрим для контроля плоскости, проходящие через грань куба. Их всего четыре. Две из них делят стороны (ребра) пополам, другие две совпадают с диагоналями квадрата.
Грань куба в октаэдре свелась к точке, но четыре плоскости симметрии остались при этом неизменными. Можно сказать, что в принципе в кубическом кристалле всегда присутствуют кубические и октаэдрические грани. Какая из этих граней появится на реальном кристалле, зависит от соотношения скоростей их роста. Ведь грань кристалла может расти только в том направлении, откуда поступает строительный материал.
Давайте-ка рассмотрим три грани: две кубические и одну октаэдрическую. Допустим, что грань куба растет вдвое быстрее, чем грань октаэдра. То, что грани куба оказываются в более благоприятном положении, на самом деле лишь допущение. В действительности все может оказаться совершенно по-другому. Ну а при сделанном нами допущении многие, вероятно, подумают: раз кубические грани растут быстрее, значит, образуется куб. Однако это очень далеко от истины. Хотя грани куба будут делаться «толще», их размер станет уменьшаться, пока они в конце концов не исчезнут совсем, уступив место грани октаэдра. Чем медленнее она будет расти, тем сильнее окажется развита на кристалле.
Существуют различные теории относительно того, почему частицы на гранях одной ориентировки осаждаются охотнее, чем на гранях другой. Но во всех случаях не следует забывать, что мельчайшие частицы отдают предпочтение углам и выступам. По этой причине они склонны наращивать «толщину» граней, имеющих не вполне гладкую поверхность. Если частицы осаждаются на неровной поверхности, ее неровности перемещаются. Одной из возможных неровностей мог бы явиться маленький поверхностный дефект спиральной формы. В процессе осаждения частиц спираль продолжает расти. Подобные спирали действительно обнаружены на некоторых кристаллах. При растворении кристаллов образование граней происходит соответственно в обратном отношении к скорости: чем быстрее удаляется материал с грани, тем она становится больше.
Одно дополнительное замечание. Вы можете встретить в учебниках такие обозначения: (100) - для кубических и (111) - для октаэдрических граней. Если даже отыскать в справочнике эти числа («индексы Миллера»), то запомнить, что они означают, не так-то просто. Рекомендуем заметить себе: грань куба пересекает одну из трех осей прямоугольной системы координат (1), а обе другие не пересекает (00). Грань октаэдра пересекает все три оси (111).
ОСНОВНЫЕ ПОСТРОЕНИЯ, ОСНОВАННЫЕ НА СИММЕТРИИ
Как разделить отрезок пополам.
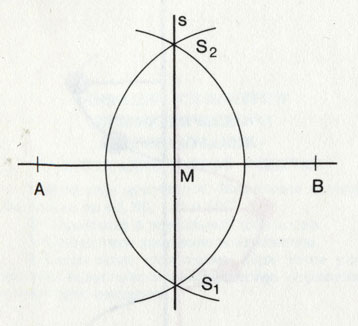
Как разделить отрезок пополам
Как разделить угол пополам.
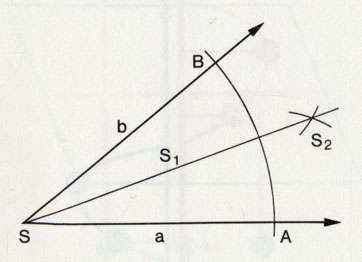
Как разделить угол пополам
Как восстановить перпендикуляр в заданной точке.
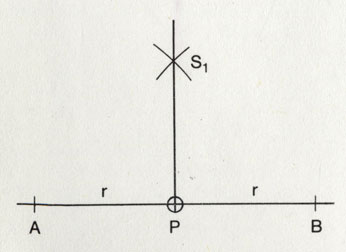
Как восстановить перпендикуляр в заданной точке
Как опустить перпендикуляр из задней точки.
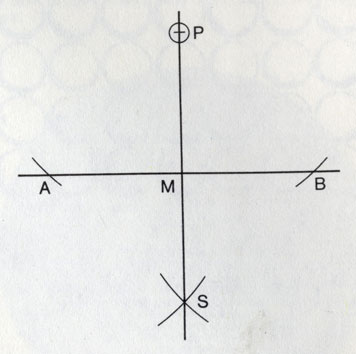
Как опустить перпендикуляр из задней точки
Как провести параллельную прямую.
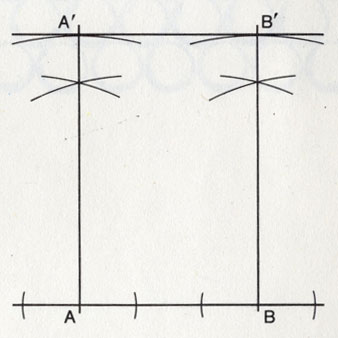
Как провести параллельную прямую
МАТЕМАТИКА ДЛЯ ПРОДАВЦОВ ФРУКТОВ
Яблоки, апельсины, грейпфруты, лимоны - излюбленные декоративные элементы оформления витрин. Для привлечения покупателей из них обычно выкладывают красочные плоские фигуры или пирамиды. Для выкладки плоских фигур могут использоваться и более мягкие фрукты и овощи - такие, как персики или помидоры.
В самом простом случае продавец фруктов или овощей ставит в витрину ящик с помидорами или персиками. Оценим наметанным глазом, соотносятся ли длины сторон ящика как 1: √ 2. «Фруктовый товар» прибывает из самых различных стран, поэтому ящики неодинаковы по величине. И все же вид этих ящиков тем привлекательнее, чем ближе их пропорции к идеальному соотношению.
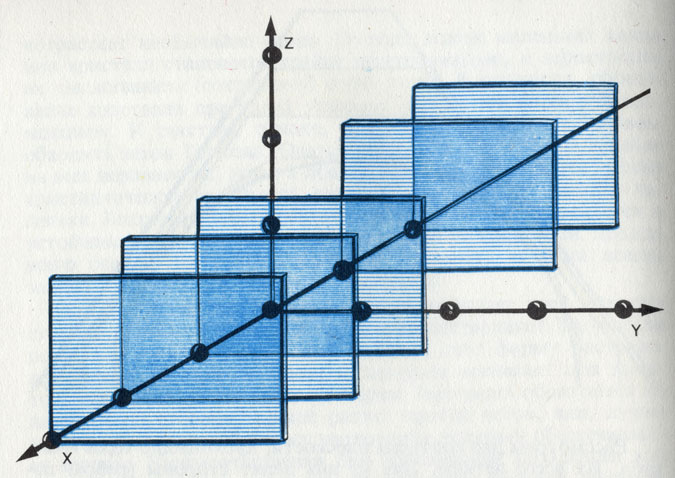
В пределах одной прямоугольной системы координат грани всегда остаются одинаковыми, на какое бы расстояние их не перемещали параллельно самим себе
Затем нас будет интересовать степень использования объема при упаковке. Цитрусовые поступают обычно с Балкан, из Африки или из других отдаленных южных краев. Перевозка их всегда стоит дорого. Поэтому фрукты должны быть упакованы не только хорошо (во избежание потерь), но и рационально, компактно (для сокращения транспортных расходов, чтобы не возрастали цены).
Возьмем ящики с помидорами. Простоты ради допустим, что все они имеют одинаково красивую форму и равную величину. Сделаем еще одно допущение - что стороны ящика имеют длину, кратную диаметру помидора. Потом возьмем и упакуем шары-помидоры так, чтобы они красиво улеглись в аккуратные прямые ряды, соприкасаясь между собой боками. В сущности говоря, упакованный подобным образом ящик сплошь состоит из квадратов, в которые вписаны круги. Площадь квадрата составляет 1Х1 = 1, если в качестве масштаба выбрать диаметр помидора. Площадь проекции помидора, напротив, равна лишь π • 0,52 = 0,785. Соответственно площадь ящика использована для укладки помидоров только на 78,5%.

При укладке ровными прямыми рядами диски или шары заполняют площадь на 78,5%
Однако на деле фрукты и овощи круглой формы бывают уложены иначе - не в прямые ряды, а в пустые гнезда. Первый ряд вдоль длинной стороны ящика касается этой стороны и прилегает к обеим ограничивающим его коротким сторонам. Пока все обстоит так же, как и в первом случае. Но второй ряд уложен в гнезда. Выигрыш очевиден и состоит в том, что помидоры теперь несколько сдвинулись кверху. Проигрыш заключается в появлении двух пустот справа и слева в конце ряда. Третий ряд, хотя и уложен тоже в гнезда второго, но представляет собой точное зеркальное отражение первого. Четвертый ряд снова отвечает второму и т. д. При укладке последнего ряда могут встретиться два случая: либо он окажется типа ряда 1, либо типа ряда 2. Во втором случае в ящик поместится на две половинки помидора меньше, чем в первом.

При плоской укладке в пустые гнезда диски или шары заполняют площадь на 90,6%
Возьмем фрагмент укладки из середины ящика. Приглядевшись, можно увидеть, что вокруг каждого кружка (помидора) располагаются шесть других кружков. Отдельные помидоры уже не вписываются в квадрат, вершина которого соприкасается с вершинами других (мысленных) квадратов, но никак не с помидорами. И четыре помидора вместе тоже не образуют квадрата: в наименьшую структурную единицу этой укладки входит всякий раз по 1/6 площади каждого из трех кругов, окружающих маленький участок свободной поверхности. Сопоставив их размеры, найдем, что степень использования площади при такой укладке возрастает до 90,6%. Это плотнейшая из известных нам плоских укладок шаров или дисков. Иначе говоря, мы не можем разместить на плоскости шары, помидоры или монеты одного достоинства (то есть размера), не оставив незанятой ее часть, равную 9,4% всей площади. Тем не менее расположение в гнездах с использованием площади в 90,6% - большое достижение по сравнению с укладкой ровными одинаковыми рядами, где этот показатель составляет лишь 78,5%.
В торговых залах больших магазинов кассы обычно устанавливаются одна за другой в длинный ряд. В случае если они больше не в состоянии совладать с натиском покупателей, их располагают «лесенкой», так удается вместить еще одну или две кассы при той же ширине зала. Станки в токарных цехах в большинстве своем сразу устанавливаются в «промежутках», чтобы возможно лучше использовать рабочую площадь.

Обычно в днище теплообменника стремятся вварить как можно больше труб, поэтому стараются расположить их наиболее рационально - в шахматном порядке: трубы верхнего ряда над промежутками между трубами нижнего ряда
Особенно важное значение имеет рациональное использование площади в теплообменниках. Теплообменник состоит из труб (в которых проходит жидкость), вваренных в общее днище. Эти трубы омываются жидкостью иной температуры. При этом температуры жидкостей вне и внутри труб выравниваются. Так как размеры всякого агрегата всегда стремятся сократить, то и трубы в теплообменниках стараются укладывать наиплотнейшим образом.
Французский мыслитель и ученый Блез Паскаль (1623-1662) посвятил шаровым упаковкам целый трактат. Он задался целью с помощью фигур (составленных из шаров) придать числам зримую наглядность. Представьте, что наш продавец фруктов вслед за Паскалем сооружает пирамиду, скажем из апельсинов. У Паскаля такая пирамида из шаров делала «зримой» третью степень. Во фруктовом магазине апельсиновая гора предназначена, естественно, не для того, чтобы напоминать нам о математике. Но если вам случилось немного задержаться в очереди у прилавка, посмотрите, как это делается. Сначала продавец выкладывает квадрат. Затем, глядя на свое произведение, он задумывается. Вы, не удержавшись, спрашиваете, над чем он ломает голову. И узнаёте, что всего лишь над тем, как из апельсинов, лежащих в этом квадрате, построить четырехгранную пирамиду. «Ну, - заявляете вы, - это ведь не так трудно. Надо попробовать». «Я уже пробовал, - отвечает продавец. - С четырьмя апельсинами не выходит, с шестнадцатью тоже, и с двадцатью пятью ничего не получается». Удивившись, вы складываете квадрат 5Х5. Потом пробуете: 3Х3=9 - в качестве основания, 4 - во втором ряду, 1 апельсин как завершение - итого лишь 14 апельсинов вместо 25, заготовленных для пирамиды. Потом вы кладете 4Х4=16 в основание, 9 во второй ряд. Это уже 25, а пирамида еще не готова. Вами обоими овладевает азарт. Продажа апельсинов прекращается. Покупателям объявляют, что они должны «принести жертву» на алтарь науки. Вы систематически перебираете все числа-квадраты - 9, 16, 25, 36, 49 и т. д., пытаясь преобразовать их в пирамиду.

При укладке в три слоя верхний слой шаров следует укладывать в гнезда между шарами среднего слоя. Если предварительно не условиться о том в какие именно ямки укладывать шары, укладка с двух сторон (навстречу друг другу) не совпадет
Наконец, либо на вас, либо на продавца нисходит то самое знаменитое «озарение»- одного из вас внезапно осеняет блестящая мысль пойти путем проб и ошибок. Вы теперь решаете задачу обратным путем, исходя не из подбора нужных размеров квадрата, а из наличия шаров - строите пирамиду сверху вниз (1, 4, 9 и т. д.) так долго, пока сумма всех использованных шаров не окажется квадратом какого-нибудь числа. Если у вас окажется под рукой карманный калькулятор, это не составит проблемы. Он быстро пересчитает вам по порядку все числа-квадраты в последовательных слоях: верхний слой 1, второй слой 4, третий слой 9 апельсинов и т. д. - и сложит результаты, то есть 1+4+9 и т. д. После каждого сложения он проверит, представляет ли собой полученное число квадрат. На 24-м слое окажется, что из 4900 апельсинов можно выложить квадрат 70Х70. Тем самым задача решена, и продавец может снять с двери табличку «Закрыто на приемку товара». Квадратное основание такой пирамиды составят 24Х24=576 апельсинов. «Давайте все же сложим маленькую пирамиду из апельсинов для витрины», - предлагает продавец. Вы с готовностью соглашаетесь и, усердно складывая апельсины, попутно объясняете продавцу, что не только в торговле возникают подобные проблемы, но, например, так же построены все кристаллы. Вам не удается закончить свои рассуждения, так как на третьем слое апельсинов, который вы с продавцом укладывали с двух сторон, узоры обеих укладок не сошлись. Решив обсудить эту проблему с продавцом, вы вконец расстроили бы торговлю. Но, может быть, вы уже поняли, в чем причина ошибки?
|
ПОИСК:
|
© NPLIT.RU, 2001-2021
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'