НЬЮТОН

Один из величайших ученых за всю историю человечества - Исаак Ньютон (1643 - 1727) оставил огромное научное наследство в самых разных областях науки. Его работы по оптике, астрономии, математике явились важнейшими этапами в развитии соответствующих наук. Но самым главным, что прославило имя Ньютона и навсегда внесло его в историю науки, было создание основ механики, открытие закона всемирного тяготения и разработка на его базе теории движения небесных тел.

Чрезвычайно важным было определение понятия силы, данное Ньютоном. Даже не зная определения силы, мы представляем себе, о чем идет речь. Слово сила ассоциируется нами с предпринимаемым усилием и вызываемыми им последствиями - толчком тачки, например, и вызванным этим толчком перемещением тачки. Некоторые ученые, и среди них, конечно, Галилей, близко подходили к тому, чтобы дать определение силы, но только Ньютону удалось это сделать. В своем замечательном труде «Математические начала натуральной философии», являющемся, вероятно, вершиной его творчества, Ньютон дал следующее определение силы. «Воздействующая сила есть действие, оказываемое па тело, чтобы изменить его состояние покоя или равномерного прямолинейного движения.

Эта сила проявляется только в действии, она не сохраняется в теле, когда действие прекращается, ибо тело сохраняет всякое повое состояние, которое оно приобретает исключительно благодаря его инерции. Воздействующие силы имеют различное происхождение: таковы силы удара, давления и центростремительные» (Цит. по: Эйнштейн Л., Инфелъд Л. Эволюция физики, с. 33.) .

В ньютоновском определении силы есть еще одно важное понятие - инерции - свойства тела, как это следует из ньютоновского определения силы, сохранять состояние равномерного прямолинейного движения или покоя. Мерой инерции тела является, как теперь принято говорить, инертная масса тела. Эйнштейн и Инфельд дают следующее определение инертной массы тела: «готовность, с какою тело отзывается на воздействие внешней силы» (Эйнштейн А., Инфельд Л. Эволюция физики, с. 33.) .

Вспомним еще раз опыт с тачкой, движущейся по горизонтальной поверхности. Оказывается, что начальная скорость тачки будет зависеть не только от первоначально приложенного усилия (силы толчка), но и от инертной массы тачки. Действительно, если тачку нагрузить больше, например увеличить ее общий вес в два раза, то при толчке одной и той же силы скорость, приобретенная более тяжелой тачкой, будет в два раза меньше.

Как измерить инертную массу тела? Можно было бы поступить следующим образом: воздействовать па два различных тела одинаковым по величине внешним усилием и измерить скорости движения этих тел; если одно тело будет иметь начальную скорость, допустим, в 5 раз большую, чем другое, то инертная масса первого тела в 5 раз меньше, чем второго. Такой способ определения инертной массы был бы логически оправдан, но он практически неудобен и поэтому не используется.

Для определения инертной массы тел применяется другой, более простой способ - взвешивание тел. Возможность его использования основана на следующем рассуждении. Земля, как известно, притягивает к себе тела, существует явление, именуемое словом «тяжесть», тело притягивается к Земле тем сильнее, чем больше его вес, больше пропорциональная весу гравитационная масса тела. Однако гравитационная масса проявляет себя совершенно иначе, чем инертная масса, и нет основании считать, что они численно равны.

Оснований для этого действительно нет (во всяком случае, не было во времена Ньютона), но зато есть опыты Галилея по свободному падению тел, о которых, мы надеемся, еще не забыл читатель и из которых следует, что все тела падают на Землю с одинаковой скоростью (если, конечно, не учитывать сопротивления воздуха).

Какой вывод может быть сделан из опытов Галилея? Нетрудно убедиться, что решающий. Действительно, при свободном падении тела на Землю увеличение его гравитационной массы должно увеличивать скорость падения, в то время, как увеличение инертной массы должно, согласно сказанному выше, уменьшать скорость падения. Из установленного опытами Галилея равенства скоростей падения па Землю всех тел может быть, очевидно, сделан один вывод: гравитационная и инертная массы тела численно равны. Заметим, что в 1971 г. советские физики Брагинский и Панов с помощью крутильных весов установили равенство гравитационной и инертной масс с точностью до 10^-12, т. е. с невероятно высокой точностью.

Законно задать такой вопрос: является ли равенство гравитационной и инертной масс случайным или оно имеет более глубокий смысл? Ответим на этот вопрос словами Эйнштейна и Инфельда: «С точки зрения классической физики ответ таков: равенство обеих масс случайно, и нет никакого смысла придавать этому факту большое значение. Ответ современной физики совершенно противоположен: равенство обеих масс имеет фундаментальный смысл и составляет новую, весьма существенную руководящую идею, ведущую к более глубокому познанию мира. Действительно, это была одна из самых важных идей, из которых развилась так называемая общая теория относительности» (Эйнштейн А., Инфельд Л. Эволюция физики, с. 32.).

Ньютон сформулировал три основных закона механики, ставшие ее фундаментом. Эти законы, именуемые законами механики Ньютона, изучаются во всех школах в начале курса физики. Несмотря на то что их содержание, несомненно, известно всем читателям, мы все же напомним его, хотя бы ради систематичности изложения.

Первый закон механики Ньютона, именуемый также законом инерции, таков: (всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока оно не вынуждено изменить его под влиянием действующих сил.) Нетрудно заметить, что первый закон Ньютона есть более строгое изложение приводившегося уже положения Галилея.

Существо второго закона механики Ньютона состоит в констатации того факта, что приобретаемое телом ускорение движения прямо пропорционально силе, под действием которой это ускорение возникает, и обратно пропорционально массе тела. Другими словами,

a = F/m,

где а - ускорение, F - сила (или векторная сумма сил), действующая па тело, m - масса тела. Или

F =mа.

Словесно второй закон механики Ньютона может быть сформулирован так: произведение массы тела на его ускорение равно действующей силе, а направление ускорения совпадает с направлением силы.

Произведение массы тела m па скорость движения этого тела v именуется в механике количеством движения или импульсом р. Следовательно,

При постоянной массе тела уравнение второго закона механики Ньютона

ma = F может быть написано в виде (Учитывая, что dp/dt=mdv/dt=ma=F)

dp/dt=F,

и поэтому второй закон механики Ньютона можно сформулировать так: изменение количества движения пропорционально приложенной движущей силе, времени ее действия и происходит по направлению действия этой силы.

Наконец, третий закон механики Ньютона: действию всегда есть равное, противоположно направленное противодействие. Или иначе: действия двух тел друг на друга всегда равны по величине и направлены в противоположные стороны.

Еще одной руководящей идеей, принадлежащей Ньютону, явился открытый им закон всемирного тяготения - один из универсальных законов природы. Согласно этому закону, все тела (Точнее говорить не о телах, а о материальных точках - идеализированных телах, масса которых принимается конечной, а размерами можно пренебречь. Ньютон понятие материальной точки не употреблял.) независимо от их свойств, а также свойств среды, в которой они находятся, испытывают взаимное притяжение, прямо пропорциональное их массам и обратно пропорциональное квадрату расстояния между ними, т. е.

где F - сила притяжения между телами (на самом деле существуют две силы, каждая из которых приложена к одному из тел; они действуют во встречном направлении, вдоль прямой, соединяющей тела), т1 и m2 - массы взаимодействующих тел, r - расстояние между ними, G - так называемая гравитационная постоянная.

В соответствии с законом всемирного тяготения происходит, в частности, падение тел па Землю, движение Луны и планет. Этот закон явился основой создания небесной механики - науки, изучающей движения тел Солнечной системы. Признание справедливости закона всемирного тяготения и его следствия - небесной механики - стало всеобщим, особенно после открытия астрономами в 1845 г. планеты Нептун, само существование которой, ее орбита и ряд характеристик, было предсказано расчетами.

В настоящее время закон всемирного тяготения служит основой для расчета движения искусственных спутников Земли и других искусственных небесных тел.

Природа сил тяготения, равно как и распространения их действия (предполагалось, что распространение тяготения происходит мгновенно), не была объяснена Ньютоном. Эти сложные вопросы получили объяснение только в созданной Эйнштейном теории тяготения.

Из того, что уже сказано о достижениях Ньютона в области механики (в том числе и небесной), об открытых им законах, видно, как много сделал для науки этот гениальный ученый. Сказанное, однако, далеко не исчерпывает областей науки, в которых работал Ньютон, и его выдающихся достижений. Мы еще вернемся к этому вопросу, а пока ознакомимся кратко с жизнью этого великого человека.

Исаак Ньютон родился 4 января 1643 г. в дер. Вулстори, находящейся в 75 км от Кембриджа, в семье мелкого фермера. Его отец умер еще до рождения сына. В 1661 г., по окончании школы, Ньютон поступил в Кембриджский университет (Тринити-колледж, т. е. Колледж троицы) и окончил его в 1665 г. При содействии известного математика, профессора Барроу, Ньютон занял лю-касовскую (Кафедра математики в Кембридже была организована па средства некоего Лгокаса, и Барроу был первым ее профессором. ) кафедру Кембриджского университета, па которой он работал до 1701 г., хотя лекции читал только до 1696 г.

Самым творческим периодом жизни Ньютона являются 60 - 80-е годы. За это время он разработал основы дифференциального и интегрального исчислений, провел опыты по разложению света, выполнил важные астрономические исследования, создал основы механики, открыл закон всемирного тяготения.

В 1668 г. Ньютон собственноручно построил зеркальный телескоп. В 1671 г. он построил второй телескоп такого же типа, но больших размеров и более совершенный. Интересно отметить, Ньютон так же, как и Галилей, обязан телескопу первым признанием своих научных заслуг.

В 1687 Ньютон опубликовал свой капитальный труд «Математические начала натуральной философии», в предисловии к которому им сказано: «...сочинение это нами предлагается как математические основания физики. Вся трудность физики, как будет видно, состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления... Было бы желательно вывести из начал механики и остальные явления природы, рассуждая подобным же образом, ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел вследствие причин, пока неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга. Так как эти силы неизвестны, то до сих пор попытки философов объяснить явления природы и оставались бесплодными. Я надеюсь, однако, что или этому способу рассуждения, или другому, более правильному, изложенные здесь основания доставят некоторое освещение» (Цит. по: Бернал Дж. Наука в истории общества, с. 265. ).

В 1696 г. Ньютон был назначен смотрителем Монетного двора, а в 1699 г.- его директором - «пост,- пишет Дж. Бернал,- который, по мнению многих, ему очень повезло получить и обязанности по которому он выполнял добросовестно» (Бернал Дж. Там же, с. 264. .) Последующие годы Ньютон жил в предместье (а теперь районе) Лондона Кенсингтоне.

В 1672 г. Ньютон был избран членом Лондонского королевского общества, в 1703 г. стал его президентом и оставался им до конца своих дней. В 1699 г. он был избран иностранным членом Парижской академии наук. За заслуги перед наукой в 1705 г. Ньютон был возведен в дворянское достоинство. Умер Ньютон 31 марта 1727 г. в возрасте 84 лет, похоронен в национальном пантеоне - Вестминстерском аббатстве.

Неудивительно, что Ньютон, крупнейший ученый-естествоисиытатель, важнейшие вопросы естественных наук рассматривал с позиций материализма. Он, например, но мнению многих ученых, считал справедливой концепцию об атомном строении вещества. Вот что говорит по этому вопросу известный японский физик Юкава: «Ньютон, с одной стороны, придерживался идеи об атомном строении вещества, восходящей еще к Демокриту, но, с другой стороны, он не отбрасывал полностью и понятия эфира: ведь в его трудах нет упоминания о материальной точке. Значит, он не думал, что атомы не имеют размеров».

В «Началах» много тревожных, полных сомнения мест. Например, обсуждение понятия массы Ньютон начинает с определения объема и задает плотность. На первый взгляд этим все ставится с ног на голову, поскольку хорошо известно, что плотность - это масса, деленная на объем, и нельзя ввести понятие плотности раньше определения массы. Действия Ньютона выглядят подозрительно, ибо не ясно, как оперировать плотностью, не имея определения массы. Но если учесть, что он придерживался атомной теории, то его изложение перестает казаться удивительным. При наличии в пространстве атомов плотность выражает их число в единичном объеме. Как определить это число - вопрос техники, а не принципа. Если в единичном объеме имеется 100 частиц, то плотность будет 100, а если 1000 частиц, то 1000» (Юкава X. Лекции по физике. М.: Энергия, 1981, с. 17 - 13.) .

Материалистический подход Ньютона следует и из разработки им небесной механики. Вот что пишет Дж. Бернал: «Созданная Ньютоном теория тяготения и его вклад в астрономию знаменуют последний этап преобразования аристотелевской картины мира, начатого Коперником. Ибо представление о сферах, управляемых перводвигателем или ангелами по приказу бога, Ньютон успешно заменил представлением о механизме, действующем на основании простого естественного закона, который не требует постоянного применения силы и нуждается в божественном вмешательстве только для своего создания и приведения в движение.

Сам Ньютон был не совсем в этом уверен и оставил лазейку для божественного вмешательства, чтобы сохранить стабильность этой системы» ( (Бернал Дж. Паука в истории общества, с. 267. ) .

И далее: «Ньютонова система Вселенной действительно представляла собой значительную уступку со стороны религиозной ортодоксальности, ибо в пей уже нельзя было столь ясно видеть руку божью в каждом небесном и земном явлении, а только в общем создании и организации всего целого» (Там же, с. 268. ).

Материалистический подход при решении многих вопросов естествознания сочетался у Ньютона с религиозностью, верой в бога. В этой связи Юкава говорит не без юмора следующее: «По Ньютону, мир сотворен Богом и приводится в движение божественным повелением и божественной волей; множество атомов тоже сотворено божеством. Мы видим здесь сотворение абсолютно неразрушимых объектов. Человек, убежденный, что после долгих трудов ему удалось создать абсолютно неразрушимую вещь,- несомненно верующий (смех в зале). Возможно, подобная вера встречается и в наши дни, но Ньютон верил не в себя, а в Бога. Его Бог - управитель, господин, законодатель» (Юкава X. Лекции по физике, с. 14. ).

И далее: «Итак, Бог-отец руководит Вселенной, одновременно он поддерживает порядок, является законодателем, а также творцом. Но как это делается, как происходит движение тел, которым управляет Бог? Как это происходит - Ньютон открыл сам. Или восстановил, как любил он утверждать» (Там же, с. 15. ).

Что касается черт характера Ньютона, то тут мления весьма различны. Дж. Бернал пишет: «В личной жизни Ньютон представлял собой чрезвычайно странную фигуру, был очень необщителен, склонен к уединению и даже скрытен. Он так и не женился и не хотел дать согласия на посвящение в духовный сан ввиду имевшихся у него сомнений насчет троицы. Ньютон знал достаточно для того, чтобы стать весьма самокритичным; однако это заставляло его быть тем более чувствительным к критике со стороны других людей» (Бернал Дж. Наука в истории общества, с. 265.) .

А из лекций Юкавы мы узнаем: «Недавно я ознакомился с другими рассказами о Ньютоне, исходящими не от физиков, а от известного экономиста Кейнса. Он разобрал и упорядочил все оставшееся после Ньютона и в результате тщательного исследования обнаружил много скрытого, не согласующегося с общераспространенным (и ложным) представлением, будто Ньютону не свойственны были живые человеческие чувства. Кейнс выявил много свидетельств обратного. Именно тогда я живо ощутил реальность существования Ньютона-человека и очень заинтересовался им» (Юкава X. Лекции по физике, с. 12.)

Даже версия о знаменитом яблоке, падение которого с дерева будто бы навело Ньютона на мысль о законе всемирного тяготения, имеет различные толкования. Друг Ньютона Стукелей утверждал, что якобы сам Ньютон говорил, что именно эпизод с яблоком помог ему открыть закон всемирного тяготения. Л другой друг Ньютона, Пембертон, выражал большие сомнения в справедливости этой версии. Он считал, что Ньютон, возможно, специально выдумал историю с яблоком, чтобы отделаться от нее в меру любопытных собеседников, может быть даже от Стукелея.

Ньютон отчетливо представлял себе всю ограниченность человеческого знания, и в этом отношении показательно одно из его высказываний, приведенное, в частности, В. И. Вернадским: «Ньютон, стариком, подводя итоги своей научной работы, говорил, что он чувствует себя в положении мальчика, разбирающего камешки на морском берегу и из этих камешков строящего детские постройки - свое мировоззрение ученого... Это чувствовал человек, который глубже других на протяжении веков научно охватил порядок природы» (Цит. но: Лихтенштейн, Е. С. Слово о науке. М., 1981, кн. 2, с. 24. ).

Имя Ньютона входит в число имей ученых, сделавших особенно много и развитии оптики (греч. optike - наука о зрительном восприятии) - разделе физики, в котором рассматриваются вопросы природы видимого излучения (света) и его распространения. Современная наука считает природу света, как и природу всех объектов и явлений микромира, двойственной - корпускулярно-еолновой. Другими словами, свет, согласно современным представлениям, обладает свойствами, присущими как потоку частиц, так и волнам. Во времена же Ньютона точка зрения на природу света только еще начала складываться, по этому вопросу шли дискуссии, высказывались различные соображения.

История развития оптики восходит ко временам, далеко отстоящим от начала пашей эры; по вопросу о природе и свойствах света известны высказывания, относящиеся к 5-му тысячелетию до н. э. В более позднее время древнегреческие ученые Пифагор, Платон, Аристотель и др. высказывали свои соображения о сущности и свойствах света. Наиболее важным результатом древнегреческих ученых было, вероятно, не столько их предположение о том, что представляет собой свет, сколько установление его прямолинейного распространения, имевшее большое практическое значение, особенно для астрономии и навигации.

Важным этапом в развитии оптики, относящимся к началу повой эры (хотя некоторые соображения высказывались раньше), было изучение преломления лучей света (рефракции) на границе различных сред (например, при прохождении через воду или стекло). Обстоятельный трактат по этому вопросу был написан Птолемеем во II в. н. э.

Наконец, Пьером Ферма (1601 - 1665), французским математиком и физиком (оптиком), приблизительно в 1660 г. был установлен принцип, носящий теперь его имя (принцип Ферма), несколько упрощенная формулировка которого может быть дана в следующем виде: истинный путь прохождения света из одной точки в другую отвечает минимально необходимому для этого времени.

Дальнейший прогресс оптики связан с именем Ньютона. Относительно природы света Ньютон придерживался корпускулярной концепции: он считал, что луч света, проходящий через межпланетное пространство, атмосферу Земли или какую-либо другую среду, представляет собой поток частиц, испускаемых источником света. В то жо время Ньютон не исключал возможности того, что свет может иметь некоторые волновые свойства, поскольку распространение его происходит, как в то время полагали, в мировом эфире - гипотетической среде, якобы заполняющей все мировое пространство,- понятие о котором потребовалось тогда для объяснения некоторых физических явлений.

Ньютон сделал очень важный шаг в понимании задолго до пего известного факта - так называемой дисперсии света, т. е. разложения обычного белого цвета на все существующие в природе цвета с образованием солнечного спектра, имеющего с одной стороны красный цвет, а с другой - фиолетовый, при прохождении луча света, например, через стеклянную призму. Ньютон дал следующее объяснение этому явлению, хорошо известному также по появляющейся иногда во время дождя радуге. Он считал, что белый цвет представляет собой совокупность различных световых корпускул (частиц), причем каждому цвету отвечает свой «сорт» корпускул. Новым в этом было прежде всего то, что, по Ньютону, различные цвета не возникали из белого цвета в стеклянной линзе или в капельках воды радуги, а были присущи белому цвету, и только проявлялись в результате преломления света (рефракции). Преломление света различно для различных цветов, составляющих белый цвет (различно для разных «сортов» корпускул). Следствие этого - возникновение солнечного спектра.

Вот что писал Ньютон по этому поводу: «...эти цвета не порождены вновь, а лишь стали видными благодаря разделению, ибо если их снова полностью смешать вместе, то они вновь составят тот свет, который они составляли до разделения, По той же причине изменения, которые получаются при соединении различных цветов, нереальны, ибо, если различные лучи вновь разъединить, они, будут проявлять точно те же цвета, как и до вхождения в смесь. Как вы знаете, синие и желтые порошки при таком смешивании кажутся невооруженному глазу зелеными, и все же цвета составляющих корпускул не изменились в действительности, а лишь смешались. Ибо, если посмотреть в хороший микроскоп, они по-прежнему будут казаться только синими и желтыми» (Цит. по: Эйнштейн Л,, Инфелъд Л. Эволюция физики, с. 83.) .

Важно отметить, что некоторые тела излучают свет только одного цвета - так называемый однородный свет. При этом различным элементам и соединениям присущи различные цвета спектра. На этом принципе построен-спектральный анализ, позволяющий определять не только качественный, но и количественный состав исследуемых веществ. Спектральный анализ нашел широкое применение в самых разных областях науки и техники, например в металлургии - для определения состава и свойств ме-талдов» и в астрономии для анализа состава небесных тел. Ньютон впервые наблюдал явление, именуемое интерферепцией света. Это явление можно видеть при определенных условиях на экране в виде чередующихся светлых и темных полос. В физике термин интерференция относят к волнам (независимо от их физической природы) и под ним понимается сложение в пространстве двух или большего числа волы, которые в различных точках усиливают или ослабляют друг друга.

Напомним, что под термином «волны» понимаются возмущения (изменения состояния) среды, распространяющиеся в этой среде без переноса вещества и несущие с собой энергию. Звук, например, распространяется в любой газообразной и жидкой среде (воздухе, воде и т. д.) посредством так называемых упругих продольных волн, представляющих собой чередующиеся зоны сжатия и разрежения.

Продольные волны (рис. 3) всегда распространяются в том же направлении, в каком происходят смещения частиц среды (например, частиц воздуха), образующие зоны сжатия и разрежения.

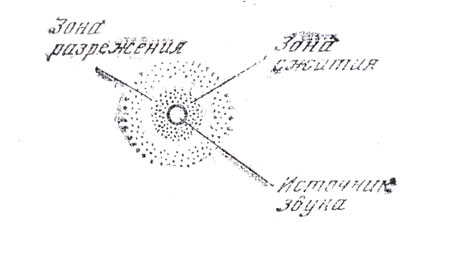
Рис. 3. Продольные волны

Если распространение волн происходит не в жидкой или газообразной среде, а, например, вдоль натянутой струны, то образуются уже не продольные, а поперечные волны (рис. 4). Дело в том, что отдельные малые участки (точки) струны будут совершать колебания от состояния равновесия не в направлении движения волны, а перпендикулярно этому направлению, поперек него. Волны, распространяющиеся по поверхности воды (или другой жидкости) также поперечны. Если на берегу озера сидит рыбак, поплавок его удочки плавает на поверхности озера, а по этой поверхности проходят волны, вызванные, например, брошенным в воду камнем (конечно, рыбак и брошенный в воду камень не очань-то вяжутся между собой), то поплавок не будет перемещаться в сторону движения волн - течение воды отсутствует, существуют только колебания воды вверх и вниз, которым и будет следовать поплавок.

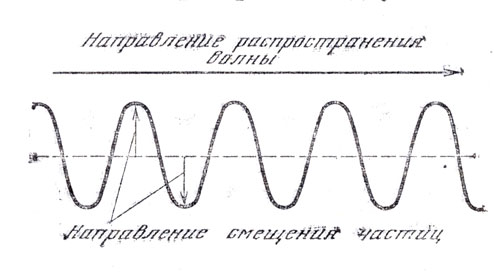
Рис. 4. Поперечные волны

Ньютон наблюдал также явление, основанное па интерференции и носящее теперь наименование колец Ньютона, а в 1675 г. дал его описание. Он исследовал явление дифракции света, рассматриваемое теперь как отклонение электромагнитных, световых волн от прямолинейного распространения, например при прохождении сквозь узкие отверстия и вблизи острых краев непрозрачных тел. Дифракция света - один из веских аргументов в пользу волновой природы света.

Представления, созданные Ньютоном о природе света и его свойствах, за прошедшие примерно 300 лет, естественно, претерпели большие изменения. Такова уж наука, она никогда не стоит на месте, старые идеи заменяются, корректируются и дополняются новыми. Это обычный и очень хороший порядок. Но как все это делается? Обесценивается ли при этом ранее внесенный в развитие науки вклад?

В ответ на эти вопросы приведем слова автора теории относительности А. Эйнштейна и его соавтора по книге Л. Инфельда: «Для сравнения мы могли бы сказать, что создание повой теории непохоже на разрушение старого амбара и возведение на его месте небоскреба. Оно скорее похоже па восхождение на гору, которое открывает новые и широкие виды, показывающие неожиданные связи между нашей отправной точкой и ее богатым окружением. Но точка, от которой мы отправлялись, еще существует и может быть видна, хотя она кажется меньше и составляет крохотную часть открывшегося нашему взору обширного ландшафта» (Эйнштейн А., Инфельд Л. Эволюция физики, с. 125) .

Для успеха в работах, которые проводил Ньютон в области физики, ему был необходим более совершенный математический аппарат, нежели имевшийся к тому времени. Эта задача была решена Ньютоном и Лейбницем, создавшими независимо друг от друга дифференциальное и интегральное исчисление - основу высшей математики, имеющее очень большое число приложений. Для этого Ньютону и Лейбницу необходимо было пользоваться понятием бесконечно малой величины - такой переменной величины, которая в процессе своего изменения становится меньше любого наперед заданного положительною числа, т. е. имеет пределом своего изменения нуль.

Ньютон рассматривал математику как абстрагированное отображение физических (механических) процессов. Он ввел два типа переменных величин: независимую переменную (аргумент), под которой понимал, учитывая, что все процессы и явления совершаются во времени, абсолютное время, и зависимую переменную (функцию)(Слово «функция» в математике отвечает двум понятиям: 1) так называется зависимая переменная, обозначаемая буквой y, 2) этим же термином именуется зависимость (функциональное уравнение), связывающая зависимую переменную величину y с независимой переменной величиной, обозначаемой x; таким образом, y=F(x).) , однозначно определяемую независимой переменной. Переменные Ньютон назвал флюентами (лат. fluo - течь, изменяться); все зависимые переменные в качестве независимой переменной имели абсолютное время. Скорости изменения флюент Ньютон назвал флюксиями. Таким образом, если под флюентой понимается скорость механического движения, то флюксия будет представлять собой ускорение - отношение бесконечно малого изменения скорости к бесконечно малому отрезку времени, в течение которого произошло изменение скорости. Отношение двух бесконечно малых величии, именуемое теперь производной (процесс определения производной называется дифференцированием), является, как этого и следовало ожидать по смыслу, не бесконечно малой, а конечной величиной. Элементарное (бесконечное малое) изменение переменной величины (например, скорости, ускорения, времени) Ньютон именовал моментом.

Ньютон является вместе с Лейбницем не только основоположником дифференциального и интегрального исчисления. Ньютону также принадлежат работы, открывшие широкие возможности применения этих новых математических методов. В их числе - определение флюксий (производных) для различных типов уравнений, связывающих зависимую переменную (функцию) с независимой (аргументом). Заметим, кстати, что если бы мы воспользовались современной терминологией (терминами, помещенными в скобках), то для современных читателей предыдущая фраза выглядела бы гораздо более удобной: в их числе - определение производных для различных типов функциональных зависимостей.

В частности, Ньютон решил задачу определения производной для степенной функции у = х^п (где х - аргумент, у - зависимая переменная функция, п - показатель степени), а также для некоторых других функций.

Ньютон и Лейбниц предложили и ввели в практику интегральное исчисление, интегрирование (лат. integer - целый), являющееся обратным действием по отношению к дифференцированию: если дифференцирование есть определение производной какой-либо функции, т. е., как следует из сказанного выше, определение предела отношения приращения функции к приращению аргумента при стремлении последнего к пулю, или производная

y′=lim (Δy/Δx)=dy/dx,
  Δx→0

то интегрирование есть определение первоначальной функциональной зависимости y=F(x) по уравнению производной y'=f(x) или ∫ƒ(x)dx = F(x) +c, где ∫ - знак интегрирования, а с - константа интегрирования.

Таким образом, если требуется, например, найти уравнение, определяющее скорость движения тела в зависимости от времени, зная как изменяется по ходу времени пройденный телом путь (именно такого рода данные, а следовательно, и расчетное уравнение можно получить опытным путем, давая телу свободно падать под действием силы тяжести), то необходимо применить дифферент циальное исчисление. Если же, наоборот, уравнение, связывающее скорость движения тела и время, известно и нужно определить зависимость пройденного телом пути от времени, то необходимо воспользоваться интегральным исчислением.

Следует заметить, что Ньютон и Лейбниц, разрабатывая дифференциальное и интегральное исчисление, использовали различный подход к проблеме; подход Ньютона можно было бы назвать физическим (у него главную роль играло понятие скорости), Лейбниц же подходил к проблеме как геометр (рассматривая задачу о проведении касательной к данной точке кривой). Естественно, что они пользовались различными символами и терминологией. В дальнейшем получили распространение символы и терминология Лейбница. Они используются в математике и в настоящее время.

Ньютону принадлежит решение важной практической задачи - преобразования некоторых функций, в том числе логарифмической, показательной (аргумент - показатель степени), некоторых тригонометрических, в бесконечные степенные ряды (так называемое разложение в ряды).

Имя Ньютона носит формула (бином Ньютона), дающая возможность представить двучлен в некоторой степени (а + Ь)ⁿв виде суммы степеней слагаемых. Например, в простейшем случае для n = 2 получается хорошо известное выражение (a+b)²= a²+2ab+b². Собственно говоря, формула, очень близкая по своему виду к биному Ньютона, была известна задолго до Ньютона. Заслуга Ньютона заключается в том, что он усовершенствовал ее, сделав применимой не только для целых, положительных значений показателя степени n, как это было раньше, но также и для дробного и отрицательного показателя.

Известны также работы Ньютона в области алгебры (в частности, данное им определение числа как отношения длин отрезков - произвольного и избранного за единицу; это определение имело немалое значение для развития представлений о действительном числе), геометрии (как аналитической, так и проективной), интерполяции (т. е. отыскания промежуточных значений какой-либо величины, заданной не уравнением, а отдельными численными значениями, в частности интерполяционная формула Ньютона, используемая и в настоящее время), вариационного исчисления (раздел математики, предметом исследования которого является определение наибольших и наименьших значений функционалов - переменных величин, зависящих от выбора одной или нескольких функций) и в других областях математики.

К сказанному хотелось бы добавить немного о методе интерполяции, пользе, получаемой от его применения в науке и технике. Воспользуемся примером. Допустим, что требуется найти какое-либо свойство и (теплоемкость, вязкость, теплопроводность, электропроводность) определенного вещества, например газа. Численные значения свойств вещества - величины переменные, зависящие от состояния вещества, в свою очередь определяемого по крайней мере двумя параметрами состояния (х, y), например температурой и давлением. На математическом языке это может быть представлено так: u=ф(x, y), т. е. свойство вещества есть некоторая функция состояния вещества (параметров состояния). К сожалению, эта функция достаточно точно неизвестна (за исключением редких частных случаев). Поэтому в большинстве случаев приходится прибегать к опытному определению численных значений и для различных х и y, в результате чего можно получить экспериментальные точки, подобные представленным на рис. 5. Здесь по оси ординат отложены значения и, по оси абсцисс - значения х различные группы точек, как это показано на рис. 5 отвечают разным значениям у: y₁, y₂, ,y_з,... Проведенная для y₁ кривая - результат интерполяции. По ней и аналогичным кривым для у2, y3, и т. д. может быть составлена таблица значений и для круглых величин х и у.

Как уже сказано, Ньютон много сделал для развития метода интерполяции. Существует также метод экстраполяции (лат. extra - сверх, вне и polio - приглаживать), отличие которого от интерполяции заключается в том, что с его помощью могут быть получены данные, лежащие за пределами исходных (отрезок кривой ab на рис. 5). Разумеется, метод экстраполяции менее надежен и точен, чем метод интерполяции.

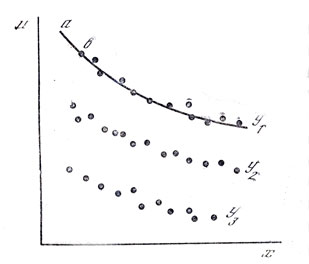
Рис. 5. Интерполяция опытных данных

Работы Ньютона охватывают очень большое число направлений физики, математики, химии. О многих из этих работ на страницах этой книги не было возможности даже упомянуть. Впрочем, такая цель и не ставилась.

В заключение приводим две выдержки из книг X. Юкавы и Дж. Бернала, X. Юкава пишет: «Обдумыванием физической картины мира занимались многие ученые мира после Ньютона: как для него, так и для них это было могучим источником интереса к нашей науке. Стремление утвердить новый взгляд на мир, создать новый образ мироздания - прекрасно, и мне кажется, что это компетенция физиков, а не философов.

Разумеется, Ньютон многое отсек у реального мира, о котором размышляют физики. Представителям других специальностей абстрактный характер механики Ньютона кажется крупным недостатком. Но это критика слабых духом, звучащая на любой стадии развития науки. Конечно, Ньютон абстрагируется, но он оставляет самое существенное и создает единую картину мира. Ему принадлежит, по крайней мере, построение теории Солнечной системы. Это один из миров. Остается еще мир неподвижных звезд (наша Галактика) и множество других миров. В них он не успел разобраться, но Солнечная система прекрасно воссоздана в рамках его механики» (Юкава X. Лекции по физике, с. 40.)

Дж. Бернал пишет по поводу труда Ньютона «Математические начала натуральной философии;»: «Галлею потребовалось, по-видимому, использовать всю силу убеждения, на которую он был способен, чтобы заставить Ньютона в течение двух лет, с 1685 по 1686 г., воплотить найденное им решение проблемы движения планет в его труде «Philosophiae Naturalis Principia Mathematical. Номинально книга была издана Лондонским королевским обществом, но Общество не имело средств, и Галлей был вынужден уплатить за издание этой книги из собственного кармана.

По убедительности аргументации, подкрепленной физическими доказательствами, книга эта не имеет себе равных во всей истории науки. В математическом отношении ее можно сравнить только с «Элементами» Евклида, а по глубине физического анализа и влиянию на идеи того времени - только с «Происхождением видов» Дарвина. Она сразу же стала библией новой науки, не столько как благоговейно чтимый источник догмы, хотя известная опасность этого и существовала, особенно в Англии, сколько как источник дальнейшего расширения изложенных в ней методов.

В своих «Началах...» Ньютон не только установил законы движения планет. Его главной целью, несомненно, было наглядно показать, каким образом всемирное тяготение может поддерживать систему мира. Однако Ньютон хотел сделать это не старым философским путем, а с помощью новой, количественной физики. При этом он должен был выполнить две другие задачи: прежде всего разрушить прежние философские концепции, старые и новые, и, во-вторых, утвердить свою собственную копцепцию не только как истинную, но и как самый точный способ объяснения явлений» (Бернал Дж. Наука в истории общества, с. 266).