
ПОСТОЯННАЯ АВОГАДРО
6. ПЕРВЫЕ ОПРЕДЕЛЕНИЯ ПОСТОЯННОЙ АВОГАДРО
Известно, какое большое значение имела для молекулярной теории и вообще для теоретической химии гипотеза или, как иногда говорят, закон Авогадро: в одинаковых объемах всех газов при одинаковом давлении и одинаковой температуре содержится одинаковое число молекул. Из этого следует, что грамм-молекула любого вещества (т. е. число граммов, равное его молекулярному весу) содержит всегда одно и то же число молекул N, названное числом, или постоянной, Авогадро. Таким образом, число Аг есть универсальная постоянная, относящаяся к любому веществу.
Одной из самых трудных проблем химии и физики второй половины XIX века было определение этого числа N.
В 1866 г. Йозеф Лошмидт (1821-1895) попытался впервые вычислить число N, исходя из кинетической теории газов. Как известно, эта теория объясняет давление газа на стенки резервуара ударами молекул газа о стенки (см. гл. 9). Из этого следует, что при прочих равных условиях давление газа будет тем сильнее, чем больше число ударов и, следовательно, чем больше число молекул, содержащихся в резервуаре. Таким образом, существует соотношение между числом Авогадро и давлением, производимым определенной массой газа при данной температуре; этим соотношением и воспользовался Лошмидт при первом вычислении числа N, конечно, пока лишь в первом приближении.
Семь лет спустя эту константу вычислил более точно Ван дер Ваальс, знаменитая формула которого лучше описывала поведение газа, заметно отличающееся, особенно при высоких давлениях, от той идеальной схемы, которая описывается законами Бойля - Мариотта и Гей-Люссака. Ван дер Ваальс нашел, что величина N должна быть больше 4,5•1023, а последующая более точная оценка дала для числа N приблизительное значение 6,2•1023.
Теория Ван дер Ваальса и вытекающие из нее следствия вызвали всеобщее восхищение, но из-за большого числа предположений, лежавших в основе как теории, так и расчета числа N, полученному значению числа Авогадро не особенно доверяли. Распространилось, однако, убеждение, психологически очень важное, что надежда получить рано или поздно достоверную и точ-яую величину N вовсе не так уже фантастична.
7. О ГОЛУБОМ ЦВЕТЕ НЕБА
Известно, что пучок света, распространяющийся в воздухе, становится видимым благодаря рассеянию на частицах пыли в атмосфере. На каждой частице свет дифрагирует тем сильнее, чем меньше длина волны падающего света. Из этого следует, что в пучке белого света дифракция будет наиболее заметной для более преломляемых лучей.
Уже в 1871 г., а в уточненной форме в 1899 г. Рэлей выдвинул предположение, что молекулы воздуха ведут себя по отношению к падающему на них пучку света точно так же, как частицы пыли, содержащиеся в атмосфере. Каждая молекула воздуха становится дифрагирующим центром, и упомянутая выше характерная для этого явления зависимость от длины волны объясняет, согласно Рэлею, голубой цвет неба. Основываясь на теории упругого эфира Френеля, Рэлей нашел отношение интенсивности прямого солнечного света к интенсивности рассеянного небом света, вытекающее из его гипотезы. В формулу Рэлея входит число N, поскольку очевидно, что это отношение должно быть тем больше, чем меньше центров дифракции, т. е. чем меньше число молекул газа, содержащихся в определенном объеме атмосферного воздуха; поэтому число N и входит в формулу.
Опытную проверку формулы Рэлея, найденной другим путем также Эйнштейном, нельзя было провести немедленно. Для этого нужны были ученые-альпинисты, ибо наблюдения приходилось проводить на большой высоте, при очень ясном небе, чтобы устранить помехи, вызываемые атмосферной пылью и каплями воды в облаках. Первые экспериментальные данные были получены лордом Кельвином (Уильямом Томсоном, 1824-1907) на основании старых опытов Квинтино Селлы, которые последний провел на вершине Монте Роза, сопоставляя одновременные значения яркости Солнца, стоящего на высоте 40° над горизонтом, и яркости неба в зените. Лорд Кельвин определил, что N должно быть не меньше 3,0•1023 и не больше 15•1023. В 1910 г. Бауэр и Мулэн с помощью специальной аппаратуры (но при плохой погоде) нашли для N значение между 4,5•1023 и 7,5•1023. Этот опыт был повторен с той же самой аппаратурой на Монте Роза Леоном Бриллюэном, который получил для величины N приблизительно 6,0•1023.
8. ВЫЧИСЛЕНИЕ ВЕЛИЧИНЫ N ПО ДАННЫМ АТОМНОЙ ФИЗИКИ
Другие способы вычисления величины N были подсказаны в конце прошлого века исследованиями субатомных процессов. В гл. 11 мы уже говорили, что величина заряда электрона равна заряду одновалентного иона при электролизе и что из этого вытекает представление о дискретной структуре электричества, как бы составленного из элементарных зарядов, имеющих величину е. Но элементарный заряд связан с числом Авогадро простым соотношением Ne=F, носящим общеупотребительное, но неточное название соотношения Гельмгольца. Здесь F - количество электричества, приходящееся на грамм-молекулу вещества при электролизе. Согласно измерениям, произведенным в конце прошлого века, F - 96 550 кулон. Эта формула применялась уже в 1874 г. Стони при вычислении элементарного электрического заряда, для которого он получил величину в 10 раз меньше истинной из-за неточного знания числа N. Но начиная с конца XIX века формулу Гельмгольца стали применять для противоположных целей: не для вычисления е, предполагая N известным, а для расчета N по измеренному значению е. Это новое применение формулы, как можно понять, объяснялось тем, что непосредственное измерение е с помощью новых методов было гораздо более надежным, чем косвенные методы нахождения величины N. Таким образом, каждое новое измерение величины е давало соответствующую величину N. Эти значения N согласовывались между собой по крайней мере по порядку величины и находились в согласии со значениями, ранее полученными другим путем.
В самом начале XX века изучение радиоактивных явлений дало более прямые способы вычисления N. Отождествив α-частицы с ионами гелия, получающимися при атомных превращениях, согласно смелому толкованию Резерфорда, о котором мы будем говорить в следующей главе, Крукс в 1903 г. сконструировал спинтарископ, получивший широкое применение. На дно небольшого цилиндра помещалось немного радиоактивного вещества примерно на расстоянии 1 см от флуоресцентного экрана, который можно было наблюдать через увеличительное стекло. На этом экране можно было видеть частые вспышки, что напоминало темное небо, на котором неожиданно загораются и потухают яркие звезды. Крукс объяснял эти вспышки столкновениями α-частиц с экраном. В 1908 г. Регенер указал, что спинтарископ можно применять для измерения молекулярных величин. Он подсчитал количество вспышек в определенном телесном угле для определенного количества полония и из этого нашел полное число α-частиц, испускаемых полонием в течение 1 сек. Затем он измерил ионный ток насыщения в воздухе, создаваемый α-частицами от того же количества полония. Еще раньше Резерфорд подсчитал, что он в 94 000 раз больше заряда, переносимого этими частицами. После этого простой арифметический подсчет дает величину заряда одной α-частицы. Этот заряд оказался вдвое больше элементарного заряда, как и должно было быть. По величине элементарного заряда с помощью соотношения Гельмгольца получается число N.
Но, несмотря на то что все эти измерения находились в согласии с ранее известными, оставалось еще некоторое сомнение в правильности истолкования Круксом причины упомянутых вспышек: можем ли мы быть уверены в том, что каждая вспышка вызывается именно одной α-частицей и что каждая α-частица вызывает вспышку, так что мы можем отождествлять число α-частиц, испущенных исследуемым радиоактивным препаратом, с зарегистрированным числом светящихся точек на экране?
Чтобы устранить это сомнение, Резерфорд и Гейгер в том же году предложили остроумнейшее приспособление, в котором летящие α-частицы попадают в ионизационную камеру только поодиночке, создаваемые ими ионы попадают на обкладку конденсатора и вызывают на соединенном с ним электрометре четко различимые импульсы, неравномерно распределенные во времени (например, от 2 до 5 в минуту). Число импульсов дает число а-частиц, которые, таким образом, легко сосчитать.
Зная это число, можно различными способами, которые и были испробованы в 1908-1910 гг., найти число N. Можно собрать α-частицы в цилиндре Фарадея, измерить их заряд и, разделив его на число частиц, получить заряд каждой из них; половина его дает нам элементарный заряд, по которому уже определяется число N. Резерфорд и Гейгер нашли таким образом значение N =6,2•1023.
Можно измерить объем, занимаемый известным числом молекул. Трудность состоит в том, чтобы собрать все α-частицы и не допустить проникновения других газов. Это удалось сделать в том же 1908 г. Джемсу Дьюару (1842-1923), более известному благодаря «сосудам Дьюара», получившим затем в обиходе название «термосов». Он определил, что 1 г радия в состоянии радиоактивного равновесия испускает за год 164 мм3 гелия в нормальных условиях. По этим данным легко получить число N=6,0•1023. Этот метод измерения был использован, правда с некоторыми усовершенствованиями, Болтвудом и Резерфордом в 1911 г., а также Кюри и Дебьерном в том же году. Полученные ими значения N совпадали с найденными Дьюаром. Если внимательно вглядеться во все эти методы нахождения числа N, то видно, что все они опирались на гипотезы, которые сейчас уже общеприняты, но в то время были предметом жарких научных споров. В самом деле, что стало бы со всей этой массой поистине восхитительных экспериментальных исследований, со всеми этими остроумными приспособлениями, со всеми этими тонкими методами, если бы было опровергнуто существование элементарного заряда или опровергнута теория атомного распада? Поэтому вполне оправданна та сдержанность, с которой все эти результаты былв встречены физиками того времени.
Следует упомянуть еще об одном имевшем огромное историческое значе-аие факте, который нужно иметь в виду, чтобы лучше понять научное развитие в первой четверти нашего века: в области радиоактивных явлений огромное большинство физиков должно было верить in verba magistri (слову учителя), потому что лишь очень немногие научные лаборатории мира располагали тогда оборудованием, необходимым для изучения радиоактивности. В первой четверти нашего века такие лаборатории были лишь в Кембридже, Манчестере, Париже, Вене и Берлине.
9. БРОУНОВСКОЕ ДВИЖЕНИЕ
Все описанные методы хорошо подтверждались исследованиями, проводившимися в совсем другом направлении и имевшими то преимущество, что они обладали гораздо большей наглядностью, поскольку относились к явлению, исследуемому уже в течение почти столетия, и опирались на прочную основу классической теории. Мы имеем в виду броуновское движение.
В 1828 г. английский ботаник Роберт Броун (1773-1858) заметил, что даже в самый простой микроскоп видно, как взвешенные в воде мельчайшие частицы находятся в непрерывном движении - удаляются, приближаются, поднимаются, опускаются, снова поднимаются, - движении очень быстром, неупорядоченном, непрестанном, буквально в вечном движении. Это явление наблюдал также Спалланцани, но связывал его с жизненными процессами, тогда как Броун признавал, что это вечное движение свойственно неодушевленным частичкам. Сначала физики не придали большого значения этому явлению, даже те, кто сам с удивлением наблюдал эти частицы и подробно их описывал. Одни говорили, что это явление объясняется дрожанием onojm, на которой находится препарат; другие - что оно аналогично движению пылинок, которое наблюдается в атмосфере, когда на них падает луч света, и которое, как было известно, вызывается движением воздуха.
Но во второй половине прошлого века по мере накопления наблюдений такая уверенность в интерпретации этого явления уступила место более критическим размышлениям. Наиболее внимательные исследователи (сам Броун, Гун, Кантони, Экснер, Винер) установили, что движение каждой частицы совершенно не зависит от соседних частиц, что оно действительно безостановочно, что какие бы меры ни принимались для соблюдения точного механического и термического равновесия раствора, движение проявляется все равно одинаковым образом, что природа или яркость применяющегося света никак не влияет на движение частиц, как не влияет на него и характер этих взвешенных частиц, а влияет лишь их масса, причем более мелкие частицы движутся быстрее.
В 1863 г. Отто Винер, подведя итог всем накопленным наблюдениям, пришел к выводу, что источником этого движения являются не сами взвешенные частицы и не какие-либо внешние по отношению к жидкости причины, а его следует объяснять внутренними движениями, присущими жидкости. Иными словами, броуновское движение обусловлено столкновениями молекул жидкости со взвешенными в ней частицами. По правде говоря, заключения Винера в том виде, в каком они появились, были очень путаными я усложненными из-за введения понятия «атомов эфира» помимо атомов материи. Но в 1876 г. Рамсей, а в 1877 г. Дельсоль, Карбонель и Тисьон, и особенно в 1888 г. Гун, ясно показали тепловую природу броуновского движения.
«При большой площади, - писали Дельсоль и Карбонель, - удары молекул, являющиеся причиной давления, не вызывают никакого сотрясения подвешенного тела, потому что они в совокупности создают равномерное давление на тело во всех направлениях. Но если площадь недостаточна, чтобы скомпенсировать неравномерность, нужно учесть неравенство давлений и их непрерывное изменение от точки к точке. Закон больших чисел не сводит теперь эффект соударений к среднему равномерному давлению, их равнодействующая уже не будет равна нулю, а будет непрерывно изменять свое направление и свою величину».
Если принять это объяснение, то явление теплового движения жидкостей, постулируемое кинетической теорией, можно сказать, представляется доказанным ad oculos (наглядно). Подобно тому как мы, не различая волн в морской дали, тем не менее объясняем качание лодки на горизонте волнами, точно так же, не видя движения молекул, мы заключаем о нем по движению взвешенных в жидкости частиц.
Это объяснение броуновского движения имеет значение не только как подтверждение кинетической теории, оно влечет за собой также важные теоретические последствия. Если мы хотим придерживаться принципа сохранения энергии, необходимо принять, что каждое изменение скорости взвешенной частицы должно сопровождаться изменением температуры в непосредственной окрестности этой частицы: эта температура возрастает, если скорость частицы уменьшается, и уменьшается, если скорость частицы увеличивается. Таким образом, термическое равновесие жидкости представляет собой статистическое равновесие.
Еще более существенное наблюдение сделал Гуи в 1888 г.: броуновское движение, строго говоря, не подчиняется второму началу термодинамики. В самом деле, когда взвешенная частица спонтанно поднимается в жидкости, то часть тепла окружающей ее среды превращается в механическую работу, так что неверно, будто такое превращение не может происходить спонтанно, как то утверждает второе начало термодинамики. Проще говоря, взвешенная в жидкости частица самопроизвольно опускается и поднимается, и неверно утверждение второго начала, что, если некое явление происходит самопроизвольно в одном направлении, оно не может самопроизвольно происходить в обратном направлении. Наблюдения, однако, показали, что поднятие частицы происходит тем реже, т. е. тем менее оно вероятно, чем тяжелее частица. Для частиц материи обычных размеров эта вероятность практически равна нулю.
Таким образом, второй закон термодинамики становится законом вероятности, а не законом необходимости (см. гл. 9). Статистическое понимание второго закона термодинамики, как известно, особенно отстаивали Клаузиус, Максвелл, Больцман, Гиббс. Но их объяснение основывалось на мысленных экспериментах (как, например, «демон» Максвелла), исходивших из постулата о реальном существовании молекул. Никакой чувственный опыт не подтверждал этой статистической интерпретации. Достаточно было отрицать существование молекул, как это делала, например, школа энергетиков, процветавшая под руководством Маха и Оствальда как раз во времена Гуи, чтобы второе начало термодинамики стало законом необходимости. Но после открытия броуновского движения строгая интерпретация второго начала становилась уже невозможной: здесь налицо был реальный опыт, который показывал независимо от какой бы то ни было молекулярной теории, что второй закон термодинамики постоянно нарушается в природе, что вечный двигатель второго рода не только не исключен, но постоянно осуществляется прямо на наших глазах.
Поэтому в конце прошлого века исследование броуновского движения приобрело огромное теоретическое значение и привлекло внимание многих физиков-теоретиков, и в частности Эйнштейна (1905 г.).
Начиная с самых первых физических исследований броуновского движения, делались попытки определить среднюю скорость взвешенных частиц. Однако полученные оценки содержали грубые ошибки, так как траектория частицы столь сложна, что ее невозможно проследить: средняя скорость сильно меняется по величине и направлению, не стремясь ни к какому определенному пределу с увеличением длительности времени наблюдения. Невозможно определить касательную к траектории в какой-либо точке, потому что траектория частицы напоминает не гладкую кривую, а график какой-то функции, не имеющей производной. Совсем недавно (в 1950 г.) У го Кассина отметил сходство между кривой Пеано и траекториями броуновского движения.
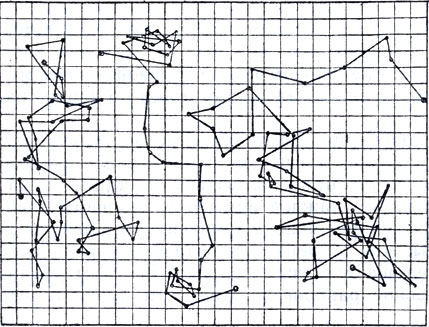
Горизонтальная проекция (в увеличенном виде) последовательных положений, занимаемых через каждые 30 сек тремя частицами камеди диаметром чуть больше 1 мк. (J. Perrin. Les atomes, 1920.)
Эйнштейн убедился в тщетности попыток определить среднюю скорость, не поддающуюся измерению, и принял за характеристику движения смещение взвешенной частицы, т. е. отрезок, соединяющий исходную точку с коцрч-ной, в которую перемещается частица за определенный промежуток времени. Ему пришла также в голову удачная мысль применить к броуновскому движению ту же гипотезу, которую Максвелл положил в основу расчета распределения скоростей молекул газа, т. е. любопытный постулат, который может показаться внутренне противоречивым: броуновское движение совершенно нерегулярно. Если принять этот постулат, то к броуновскому движению можно применить те же рассуждения, которые использовал Максвелл при изучении скоростей молекул (см. гл. 9), и прийти вместе с Эйнштейном к заключению, что в суспензии мельчайших частиц (или в эмульсии) так же, как в растворе, наблюдается диффузия с вполне определенным коэффициентом диффузии, зависящим от температуры эмульсии, числа Авогадро, размера частиц эмульсии (предполагаемых равными между собой) и вязкости жидкости. Отсюда следует, что если можно измерить все другие величины, то по данной Эйнштейном формуле можно непосредственно вычислить величину N.
Это легче сказать, чем сделать; трудности, которые нужно преодолеть при этих экспериментах, действительно огромны. Первые опыты не дали убедительного результата. Более того, данные киносъемки броуновского движения (первый случай использования киносъемки при изучении физических явлений), произведенной в 1908 г. В. Анри, казалось бы, противоречили теории Эйнштейна и привели многих нетерпеливых физиков к заключению, что в этой теории, должно быть, неявно принята какая-то неверная предпосылка. Но в том же году Ж. Перрен, ученый, обладавший редким даром экспериментатора, взялся за ее проверку, избрав очень удачный метод исследования. И действительно, ему удалось, следуя Эйнштейну, вычислить N, подойдя к изучению броуновского движения совсем с другой стороны.
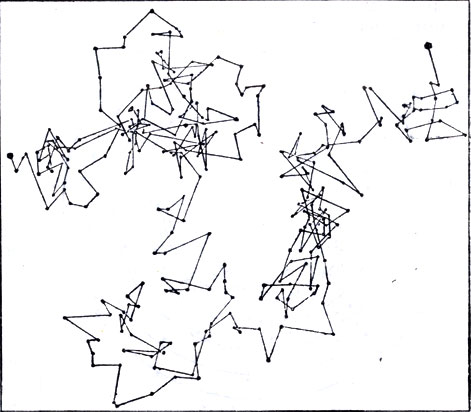
Большое число перемещений одной частицы камеди, полученных тем же способом, как и на предыдущем рисунке. (J. Реrrin, Les atomes, 1920.)
Перрен начал с проверки основной гипотезы теории Эйнштейна, т. е. предположения о совершенной нерегулярности движения. Он наблюдал в освещенной камере последовательные положения одной и той же частицы эмульсии через равные промежутки времени. Для примера на помещаемых здесь рисунках отмечены положения, которые последовательно через каждые 30 сек занимала частичка камеди диаметром чуть больше одного микрона. Разумеется, если бы отметки делались через каждую секунду, то каждый отрезок фигуры был бы заменен ломаной из 30 отрезков, что дает нам представление о поразительной запутанности реальных траекторий частиц. Если движение совершенно нерегулярно, то проекции этих отрезков на какую-либо горизонтальную ось должны располагаться вокруг их середины по случайному закону, выражаемому известной математической формулой. Полученные по этой формуле значения поразительно совпадали с результатами экспериментов.
Ланжевен предложил более простой способ проверки совершенной нерегулярности броуновского движения, применив метод параллельного переноса наблюдаемых смещений так, чтобы начала всех смещений находились в одной точке. Если движение действительно совершенно нерегулярно, т. е. подчиняется законам случайности, то концы смещений, перенесенных так, чтобы «х начала совпали, должны расположиться вокруг их общего центра, как располагаются при стрельбе попадания пуль вокруг центра мишени. Произведя такое геометрическое построение на основании 500 наблюдений, проводившихся с интервалом в 30 сек, Перрен получил картину, воспроизведенную на рисунке на стр. 350. Разве, взглянув на этот рисунок, читатель не подумал сразу же, что перед ним стрелковая мишень, продырявленная пулями целого батальона солдат?
Проверив основной постулат, Перрен и его сотрудники провели семь серий измерений диффузии эмульсий, изменяя различным образом условия опыта. Подстановка полученных результатов в формулу Эйнштейна дала в качестве наиболее вероятного значения N величину 6,85•1023.
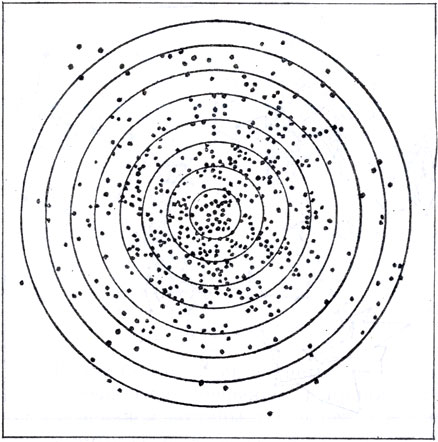
Распределение конечных точек горизонтальных смещений частицы камеди, перенесенных параллельно самим себе так, чтобы начала всех смещений? находились в центре окружности, (3. Реrrin, Les atomes, 1920)
Этой проверке, как мы уже говорили, предшествовала другая аналогичная работа Перрена. Учитывая, что Вант-Гофф распространил на разбавленные растворы законы газов, Перрен пришел к следующему заключению:
«Молекула сахара, содержащая 45 атомов, и молекула сульфата хинина, содержащая свыше 100 атомов, играет в растворе не большую и не меньшую роль, чем какая-нибудь молекула воды, содержащая всего лишь 3 атома.
А раз так, разве нельзя предположить, что не существует никакого предельного размера атомов, для которого справедливы эти законы? Разве нельзя предположить, что даже видимые частицы и те подчиняются этим законам, так что частица, подверженная броуновскому движению, играет не большую и не меньшую роль, чем обычная молекула в процессе соударения со стенками сосуда? Короче говоря, разве нельзя предположить, что законы газов применимы также и к эмульсиям, состоящим из видимых частиц?» (Jean Реrrin, Les atomes, Paris 1920, p. 128-129 (первое издание вышло в 1913 г.) )
Перрен решил, что истинность этой гипотезы проще всего проверить, исследовав распределение частиц эмульсии по высоте. Если законы газов действительно применимы к эмульсиям, то, подобно тому как число молекул воздуха убывает с высотой, число частиц эмульсии должно также уменьшаться с высотой. Известно, что с высотой воздух становится более разреженным, потомучто верхние слой воздуха давят своей тяжестью на нижние (см. гл. 5). Полагая, что разница между давлениями на двух границах горизонтального слоя воздуха обусловлена весом этого слоя, Лаплас путем простейшего подсчета вывел закон зависимости плотности атмосферы от высоты и вообще закон распределения плотности произвольного газа, подверженного одной лишь силе тяжести. Закон Лапласа носит экспоненциальный характер и утверждает, по существу, что одинаковой разности уровней соответствует одинаковая степень разрежения, пропорциональная молекулярному весу рассматриваемого газа. Например, для кислорода при 0° С плотность уменьшается вдвое при подъеме на каждые 5 км, а для водорода, чтобы получить такое же уменьшение плотности, подъем должен быть в 16 раз большим, потому что грамм-молекула водорода в 16 раз легче грамм-молекулы кислорода.
Если на эмульсии распространяются те же законы, что и на газы, то распределение частиц по высоте должно подчиняться закону Лапласа (с соответствующими изменениями). А именно, если все частицы эмульсии одинаковы, как это имеет место для молекул, то «грамм-молекула частиц» получится умножением числа Авогадро на массу одной частицы. Аналогом плотности газа будет насыщенность эмульсии частицами, т. е. количество частиц, содержащихся в заданном объеме. Если опыт подтверждает, что эмульсия ведет себя подобно газу, то применение к ней формулы Лапласа позволяет найти число N по данным измерений других характерных величин.
Трудности, возникающие при проведении таких опытов, очевидны: выбрав подходящую эмульсию (Перрен после нескольких проб остановился на эмульсии камеди или древесной смолы), нужно добиться, чтобы все частицы, имея микроскопические размеры (диаметр меньше полмикрона), были одинаковой величины; нужно далее определить их плотность и массу и произвести микроскопическое исследование распределения частиц по уровням в пределах десятой доли миллиметра, подсчитав количество частиц на различных уровнях. Доказательством того, что совершенство и точность опытов Перрена вполне соответствовали трудностям стоявших перед ним задач, служит совпадение результатов различных серий измерений, проведенных как самим Перреном, так и его сотрудниками. Результаты исследования эмульсий показали, что частицы распределяются в соответствии с предсказаниями теории, и по данным опытов была получена для N средняя величина 6,82•1023, с возможной ошибкой, которая по оценке Перрена составляла 3%,
10. ВЫВОД ЧИСЛА АВОГАДРО ИЗ ТЕОРИИ КВАНТОВ
Из всего сказанного ясно, какое значение для науки в самом начале нашего века имело число N, причем не только для теоретической химии, но и для наиболее новых разделов физики того времени. Достаточно указать, например, что каждое уточнение значения величины N влечет за собой изменение молекулярных величин, и в частности изменение величины элементарного* заряда, связанного с N через уравнение Гельмгольца.
Вот почему немаловажное значение имеет тот факт, что величину TV можно подсчитать по формуле излучения черного тела, предложенной7 Планком. Но этот первый успех теории квантов, конечно, гораздо яснее сейчас, чем это было в те времена. Тогда, в 1901 г., когда этот подсчет был проделан Планком, имелись лишь немногочисленные и неточные данные о величине N. Определение числа N не могло ни поднять авторитет квантовой теории, потому что не было известно точное значение N, с которым можно было бы сопоставить вновь полученное, ни придать большую достоверность ранее полученным значениям N, потому что сомнению подвергалась как раз сама теория, с помощью которой проводился расчет. Этими обстоятельствами и объясняется тот факт, что в первое десятилетие нашего века расчету N, проведенному Планком, не придавали большого значения. Мы же, чтобы подчеркнуть значение этого первого успеха квантовой теории, слегка нарушили хронологическую последовательность изложения.
На первый взгляд может показаться парадоксальным, что закон излучения, т. е. закон, относящийся к явлению, наблюдающемуся при отсутствии всякой материи, содержит в себе величины, относящиеся к структуре материи. Этот кажущийся парадокс вытекает из того факта, что в теории Планка фигурируют законы статистической термодинамики, в которые входит коэффициент, не зависящий от системы и имеющий, следовательно, такое же значение и для газов. Вот почему в формулу входит число N, как это видно из примечания на стр. 338.
В действительности Планк пользовался не только этой формулой, но и законом Стефана и законом смещения Вина (которые, впрочем, легко выводятся из его формулы излучения) и получил для N величину 6,16•1023, в прекрасном соответствии с наиболее достоверным в то время значением, найденным Ван дер Ваальсом.
Чтобы иметь возможность лучше судить о ценности полученных результатов, закончим этот параграф указанием на то, что один из лучших известных сегодня способов определения N основан на данных по дифракции рентгеновских лучей и что принятое в настоящий момент значение N равно 6,02•1023.
Возможная ошибка не превышает одной тысячной, т. е., по образному выражению Милликена, постоянная Авогадро известна сегодня с большей точностью, нежели можно знать в какой-либо определенный момент количество жителей в таком городе, как Нью-Йорк.
http://teplosity.ru/ каталог Шаровых кранов aquarius УЗТПА.
|
ПОИСК:
|
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'