
ОПТИКА
16. ОПТИКА КЕПЛЕРА
Физика XVII века фактически состояла из двух разделов - механики и оптики, для которых общей областью применения была астрономия. Чтобы удовлетворить нужды астрономии, Иоганн Кеплер (1571-1630) написал фундаментальный труд по оптике «Ad Vitellionem paralipomena, quibus astronomiaepars optica traditur» («Паралипомены к Вителлию»), 1604г., который он скромно рассматривал (это видно из самого названия) как простое дополнение к оптике Вителлия, т. е. (см. гл. 2) к оптике Аль-хазена. Кеплер неоднократно говорил, что его вдохновляли семнадцатая книга «Магии» и трактат «О преломлении» Порты, которым он приписывал значительно большие достоинства, чем склонны признавать современные критики. Интересно заметить, что многие идеи Кеплера встречались у Мавролика, работы которого по оптике тогда еще, впрочем, не были опубликованы (см. гл. 3).

Иоганн Кеплер. Портрет кисти неизвестного автора
Из этой работы Кеплера для нас интересны первые шесть глав, поскольку последние пять глав посвящены астрономическим проблемам. В соответствии с идеями Альхазена Кеплер изгоняет из оптики всякие «призраки» и «образы» и рассматривает конусы лучей, исходящих по всем направлениям из каждой светящейся точки. С помощью этих лучей он объясняет задачу, которая оставалась покрытой тайной для всех предшествующих оптиков. Почему мы видим в зеркале изображения там, где их заведомо нет? Потому, отвечает Кеплер и вместе с ним современные физики, что глаз, воспринимающий лучи, не может знать, какой путь они прошли, и помещает светящуюся точку на их продолжении. Аналогичное объяснение дается локализации изображения, видимого при преломлении; таким образом легко объясняется опыт с кажущимся переломом опущенной в воду палки, остававшийся необъясненным в течение тысячелетий - «macula foeda in pulcherrima sciential («черное пятно в прекраснейшей науке»), как говорил Кеплер.
Пятая глава работы Кеплера посвящена преломлению. С помощью остроумного экспериментального приспособления он пытался найти закон преломления, но в конце концов удовлетворился тем, что вернулся к старому правилу, приписываемому Птолемею (см. гл. 1): для углов меньше 30° угол падения пропорционален углу преломления. И все же даже это правило пригодилось ему при исследовании преломления в шаре, когда он вводит новый очень важный экспериментальный метод. Кеплер сознает, что это не одно и то же - рассматривать изображения глазом или же получать их на экране, и догадывается, что второй метод значительно упрощает эксперимент, который становится более объективным. Одним словом, он заменяет средневековую физиологическую оптику современной геометрической. Комбинируя этот метод с идеей Даниэля Барбаро о диафрагмировании сферы (см. гл. 3), Кеплер приходит к фундаментальному открытию: при преломлении лучей, проходящих через задиафрагмированную сферу, одна точка изображения соответствует также одной точке предмета, а параллельный пучок лучей «сходится», «конвергирует» (ему принадлежит и применение этого термина) в точке, которой он дал название фокус.
Пятая глава - самая знаменитая в работе Кеплера. В ней рассматривается механизм зрения. Кеплер оказался смелее Альхазена, Мавролика и Порты и продолжил ход лучей света до сетчатой оболочки. Он понимал, что изображение на сетчатой оболочке обязательно будет перевернутым, но считал, что из этого факта вовсе не следует, что мы должны видеть предметы перевернутыми: достаточно, чтобы глаз помещал светящую точку вверх, когда образующееся в глазу изображение находится внизу, и помещал эту точку справа, когда оно находится слева, и наоборот.
Среди ученых того времени работа Кеплера не вызвала большого интереса. В 1610 г. Галилей еще, несомненно, не знал о ней, так что ее влияние на создание и тем более на применение подзорной трубы следует исключить.
Более того, из неопределенного отношения Кеплера к первым сообщениям об астрономических открытиях Галилея следовало бы сделать вывод, что он даже не очень доверял подзорной трубе. Однако эта нерешительность Кеплера, впрочем не совсем неоправданная, вскоре была искуплена его восхищением астрономическими открытиями Галилея и написанной им в августе - сентябре 1610 г. и опубликованной в 1611 г. «Диоптрикой», целью которой было дать теорию подзорной трубы, подкрепив математическими доказательствами данные чувств.
«Диоптрика» основана на геометрической оптике, изложенной в «Паралипоменах», однако она расширяет и уточняет ее и прежде всего применяет к исследованию лииз, действия хрусталика глаза, коррекции близорукости и дальнозоркости. Затем Кеплер переходит к рассмотрению комбинации нескольких линз, четко формулируя положение о том, что изображение от одной линзы может служить предметом для другой. Результаты рассмотрения он применяет в конструкции подзорной трубы с выпуклым окуляром, называемой теперь кеплеровой, или астрономической, впервые реализованной, по-видимому, в 1630 г. Шейнером (1575-1650. Кеплер рассматривает также прибор, который называется сейчас телеобъективом, и, наконец, дает теорию подзорной трубы Галилея.
17. ЗАКОНЫ ПРЕЛОМЛЕНИЯ
В упомянутых двух работах Кеплера была построена современная элементарная геометрическая оптика. Однако здесь не хватало одного основного закона - закона преломления. Астрономические открытия Галилея придавали оптике весьма большую актуальность, а труды Кеплера вырвали большую часть ее, и особенно теорию зрения, из-под власти философии.
В такой обстановке начал свои исследования по оптике Декарт, воодушевленный изобретением подзорной трубы, задавшийся целью улучшить ее конструкцию (что ему, впрочем, не удалось) и, по-видимому, питавший надежду соперничать с Галилеем и превзойти его в астрономических открытиях. Он отдавал себе отчет в том, что фундаментальной проблемой новой науки является теория света. И действительно, первая глава его «Диоптрики» носит многообещающее заглавие «О свете». Но, к сожалению, это лишь название. Перед лицом сложной проблемы одной научной фантазий философа недостаточно. Пообещав объяснить «все» уже известные свойства света и вывести «все» другие свойства, он тем не менее заявляет, что ему незачем вскрывать истинную природу света, для его целей, т. е. для объяснения зрения и действия подзорной трубы, ему достаточно использовать две-три аналогии. Первая аналогия-двухтысячелетней давности: как слепой, нащупывая своей палкой, создает себе представление о предметах, так и свет «является неким движением или неким действием», которое через воздух и другие прозрачные тела идет от светящегося тела к глазам. Вторая аналогия, противоречащая предыдущей, говорит о материальной природе света: как два потока виноградного сусла вытекают, не мешая друг другу, из двух отверстий в дне чана, полного винограда, так и потоки тонкой материи, исходящей из Солнца к нашим глазам, не возмущают друг друга и не возмущаются обычной материей. Третья аналогия - это аналогия Альхазена: световой луч подобен брошенному материальному телу.
С помощью этих трех аналогий, используя то одну, то другую, Декарт рассматривает прямолинейное распространение света, прохождение света через прозрачные тела, отражение, рассеяние. Нельзя сказать, чтобы его идеи были «ясными и отчетливыми», поскольку в конце концов так и не удается установить, чем же является для Декарта свет: объективным или субъективным явлением, движением или материей? Эта первая глава «Диоптрики» столь непонятна и путанна, что математик, и к тому же картезианец, Христиан Гюйгенс вынужден был признаться, что не понимает, что хотел сказать Декарт о природе света. Ученые пришли к выводу, пожалуй чересчур уж поспешному, что «Диоптрика», представленная Декартом как пример применения его «метода», есть как раз свидетельство несостоятельности последнего [как известно, знаменитая работа Декарта, опубликованная в 1637 г.. носила название «Discours de la Methode pour Ыеп conduire sa raison, et chercher la verite dans les sciences. Plus la Dioptrique les Meteores et la Geometric qui sont des essais de cette Methode» («Рассуждение о методе как средстве направлять свой разум и отыскивать истину в науках. С приложениями: Диоптрика, Метеоры и Геометрия, которые дают примеры этого метода»)] (Есть русский перевод: Р. Декарт, Рассуждение о методе, Л., 1953).
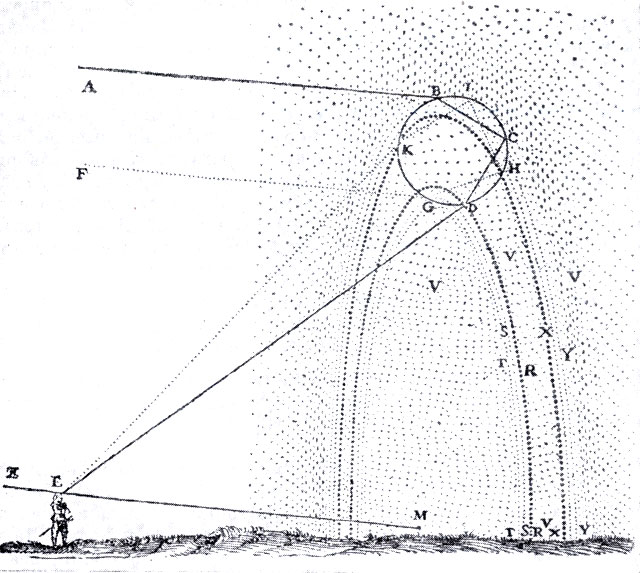
Декартово объяснение радуги. Солнечный луч АБ преломляется, распространяется, отражается в капле воды и попадает к наблюдателю окрашенным по пути DE
Во второй главе говорится о законах отражения и преломления, но не света, а брошенных тел, с последующим обобщением, разумеется произвольным, на свет. В ней содержится ряд важных результатов. Декарт рассматривает мяч, брошенный на слабую сетку; пусть он прорывает ее, теряя часть скорости, скажем, половину. Тогда, говорит Декарт, движение мяча «совершенно отличается от его предназначения в одну или в другую сторону».
Можно представить себе, что это «предназначение» составлено из двух частей: одной, побуждающей мяч двигаться сверху вниз, другой - слева направо. На современном языке все это, очевидно, означает, что фактическое движение можно представлять как результирующую двух составляющих движений. Горизонтальная составляющая не меняется, так как сетка не препятствует движению тела в этом направлении, тогда как вертикальная составляющая меняется, потому что в этом направлении сетка препятствует движению. Изменение одной из составляющих как раз и вызывает изменение направления движения мяча. Это рассуждение позволяет Декарту прийти с помощью простых геометрических рассуждений к закону преломления, которого безуспешно доискивались в течение тысячелетий: отношение синуса угла падения к синусу угла преломления есть величина постоянная.
Но в рассуждении Декарта есть один порок: более плотная среда обычно сильнее преломляет (во времена Декарта полагали, что это всегда так), поэтому Декарт должен был заключить, что скорость света в более плотных средах больше. В то же затруднительное положение попадет впоследствии и Ньютон, но он просто обойдет эту трудность. Декарт же хочет найти объяснение этому странному факту и предается рассуждениям, столь туманным, что мы снова должны согласиться с Гюйгенсом - понять, что подразумевает Декарт под светом, невозможно.
Лейбниц, Гюйгенс и многие другие обвинили Декарта в плагиате, поскольку закон преломления был открыт экспериментально Виллебродом Снеллиусом (1591-1626), излагавшим его на лекциях в Лейдене, и эти лекции Декарту были известны. Но обвинение не было подтверждено документами. К тому же в рассмотрении Декарта истинным открытием является разложение скорости света на составляющие. А эту ключевую идею Декарт заимствовал у Альхазена (см. гл. 2), так что открытием своего закона Декарт больше обязан этому арабскому физику, нежели голландскому ученому.
Декарта обвиняли также в противоречиях, поскольку он, как и Кеплер до него, считал скорость света бесконечной, а затем в случае преломления разлагал ее на две составляющие, одна из которых менялась: это означало, очевидно, что он полагал скорость конечной.
Это противоречие, по нашему мнению, можно объяснить без всякого мудрствования, если вспомнить об утилитарных сторонах науки, которые означают всегда известную долю эмпиризма, того самого эмпиризма, который позволил, например, Ньютону допустить действие на расстоянии, хотя он был убежден, что даже бог не может действовать на расстоянии. В теоретическом плане Декарт должен был принять бесконечность скорости света, потому что конечная скорость, складываясь со скоростью Земли, привела бы к явлению, названному позже «аберрацией» и обнаруженному Бредли лишь в 1725 г. Но, размышляя над страницами трудов Альхазена. Декарт в 1627 г. открыл простой закон преломления, безуспешно разыскивавшийся веками. Найдя этот закон, он его сопоставил с многочисленными экспериментами, применил для отыскания профилей линз, которые он считал наилучшими, и использовал для объяснения радуги. Короче говоря, Декарт дал жизнь многочисленным следствиям этого закона. Неужели он должен был отказаться от него только потому, что он вытекал из модели, не согласующейся с его теоретическими представлениями? Декарт прямо говорит, что все его модели неверны или ненадежны, но все же верит, что из них можно вывести правильные и полезные следствия,
«подражая в этом астрономам, которые, хотя их предположения почти всегда ошибочны и недостоверны, делают весьма правильные заключения, опирающиеся на различные выполненные ими наблюдения» (Oeuvres de Descartes, цит. выше, VI, р. 83).
В общем, по нашему мнению, даже рационалист Декарт оказался в этом случае в рядах многочисленных «физиков-оппортунистов», к которым принадлежали в этом веке Паскаль, Гюйгенс и Ньютон, если называть лишь крупнейших.
Прежде чем говорить о блестящем применении закона преломления для объяснения радуги, мы должны остановиться на принципиально новом подходе к пониманию цветов в первой главе «Диоптрики». У физиков первой половины XVII века свет был бесцветным в буквальном смысле слова. Даже Кеплер считал, что цвет - это вещь, совершенно отличная от света, некое «качество», которое должны продолжать изучать философы. А философы говорили о цвете такие вещи, которые совершенно непостижимы для нас сейчас: что цвет есть качество, пребывающее на поверхности непрозрачных тел; что он существует в предвидении, видим в потенции и становится види-мым в действии внешнего света; что между прозрачным и непрозрачным существует различие ограничения, и прочее, и прочее.
Но Декарт знает, что вторичные качества пребывают в ощущающем субъекте, поэтому он выбрасывает за борт все эти философствования и утверждает, что мы различаем цвета по различным способам воздействия света на наши глаза. Более явно это звучит в гл. VIII «Метеоров»:
«Природа цвета заключается лишь в том, что частицы тонкой материи, передающей действие света, стремятся с большей силой вращаться, чем двигаться по прямой линии] таким образом, те, которые вращаются с гораздо большей силой, дают красный свет, а те, которые вращаются лишь немного сильнее, дают желтый... И во всем этом рассуждение так хорошо согласуется с опытом, что, по-моему, хорошо познав то и другое, невозможно сомневаться в том, что дело происходит именно так, как я это сейчас объяснил» (Там же, р. 333, 334).
Оставляя в стороне детальный физический анализ этого отрывка, обратим внимание лишь на принципиально новое фундаментальное представление: цвет - это физико-физиологическое явление, обязанное различным ощущениям, вызываемым различным движением светоносных частиц.
Одной из наибольших удач Декарта как экспериментатора были его опыты по исследованию образования радуги, описанные в гл. VIII «Метеоров». Во всех современных работах приводится объяснение радуги Декарта, которое было дополнено Ньютоном. Ученые XIX века (Юнг, Эйри и Пернтер) оставили без изменения это объяснение и лишь уточнили его, учтя явления интерференции и дифракции, неизвестные во времена Декарта. В современных работах этот вопрос излагается сравнительно просто, без привлечения данных эксперимента, что достигается благодаря использованию представления о наименьшем отклонении, введенного в оптику только Ньютоном и особенно разработанного в 1725 г. Эйлером. Декарт же, который, не зная принципа наименьшего отклонения, должен был сначала произвести опыты со сферическим стеклянным сосудом, заполненным водой и помещенным на солнце. При этом оказалось, что если линия зрения, идущая к какой-либо точке сосуда, образует угол около 42° с направлением падающих лучей, то эта часть сосуда кажется ярко-красной; если этот угол чуть меньше, то появляются последовательно другие цвета. Затем с помощью небольшого экрана, которым он закрывал различные части сосуда, ему удалось выделить пучок падающих лучей, который мы теперь называем пучком в положении наименьшего отклонения, и проследить его путь внутри сосуда. Вот тут Декарт для разъяснения своих идей о природе радуги проводит сравнение появления окраски на сферическом сосуде с появлением окраски при прохождении лучей через призму. Это позволяет ему построить на основе эксперимента свою теорию цветов, о которой мы упоминали выше. При этом закон преломления дает возможность объяснить с помощью длинного численного подсчета, как получается этот вполне определенный угол в 42° между падающими лучами и лучами, исходящими из сосуда. Таким образом, объяснение радуги получено в результате серии опытов, хорошо задуманных, тщательно проведенных и подкрепленных расчетом-истинный шедевр современного физического исследования!
18. ПРИНЦИП ФЕРМА
Излагая историю этого принципа, значение которого в новое время особенно подчеркнула волновая механика, мы остановимся на некоторых деталях, достаточно хорошо иллюстрирующих медленность усвоения определенных идей (сейчас представляющихся очевидными), и в то же время извилистость и запутанность того пути, каким иной раз физика приходит к установлению своих принципов.
Еще до опубликования «Диоптрики» Декарта Мерсенн направил Пьеру Ферма (1608-1665) первые главы ее, спрашивая его мнение о них. И уже в сентябре 1637 г. Ферма ответил, высказав в основном два замечания по методу Декарта. В первом он ставил в вину Декарту то, что тот произвольно переносит на распространение света свойства движения брошенных тел, поскольку скорость последних конечна и переменна, тогда как свет распространяется мгновенно. Во втором замечании Ферма отвергает принцип разложения движения на составляющие, который он, как видно, не понял и к которому всегда относился с подозрением. Даже через 20 лет, в 1657 г., он писал, что нужно соблюдать осторожность в применении составных движений, уподобляя их лекарствам, которые становятся ядами при неправильном употреблении.
После возражения Декарта, переданного опять-таки через Мерсенна, Ферма по-прежнему настаивал на своих критических замечаниях и отрицал главным образом пользу и законность принципа разложения движений; кроме того, он недопонимал декартово понятие «предназначения» («determination»), которое было для него эквивалентно просто направлению, тогда как Декарт употреблял его в смысле вектора скорости. В декабре 1637 г. полемика между этими двумя учеными фактически закончилась двумя письмами Ферма, одним Декарта - и каждый остался при своем мнении.
Но Ферма продолжал размышлять на эту тему и изложил свои соображения в «Рассуждении», к сожалению утерянном, направленном его другу Кюро де ла Шамбру. Эти соображения должны были еще раз подкрепить убеждение в ошибочности законов преломления Декарта или по крайней мере в несостоятельности его доказательства. Это Ферма подтверждает в энергичном письме к картезианцу Клерселье, написанном в 1658 г., в котором он вновь выдвигает свои старые возражения и добавляет еще одно: нет никаких оснований считать, что касательная составляющая скорости во второй среде должна оставаться неизменной, потому что вторая среда обладает иными свойствами.
Но при возобновлении спора с картезианцами ход мыслей Ферма уже изменился. На это повлияло чтение книги по оптике де ла Шамбра, в которой законы отражения выводятся по методу Герона (гл. 1), т. е. с помощью метафизического принципа, согласно которому природа всегда действует по кратчайшему пути, - общего принципа, достаточно неопределенного, чтобы его можно было всегда надлежащим образом приспособить к конкретным случаям. Ферма тотчас стал искать такую формулировку принципа, которая успокоила бы научную совесть его друга, обеспокоенного тем, что в ряде известных случаев отражения от вогнутых зеркал природа действует по самому длинному пути. Ферма уверял, что в этих случаях под более коротким путем следует понимать путь более простой; следовательно, поскольку прямая проще кривой, луч света, падающий на вогнутое зеркало, следует относить к плоскости, касательной к зеркалу в точке падения, а отсюда вытекает, что отнесенный к этой плоскости путь луча всегда самый короткий. Нельзя сказать, чтобы это рассуждение было особенно ясным! Если этот принцип объясняет так хорошо все случаи отражения, почему бы его не применить также и к преломлению? Если луч света идет из точки А в точку С, преломляясь в точке В, то его путь ABC, конечно, длиннее, чем А С. Но принцип экономии в природе следует понимать в том смысле, что кратчайшие пути - это наиболее легкие, т. е. пути наименьшего сопротивления. А если предположить, что сопротивление второй среды распространяющемуся свету отличается от сопротивления первой, то может оказаться, что путь ЛВС соответствует в целом меньшему сопротивлению, чем путь АС. Эта идея - первый зародыш идеи, приведшей к формулировке принципа Ферма, - была, несомненно, весьма остроумной, но тотчас вступила в противоречие с убеждениями ученого. Действительно, понятие сопротивления сразу влечет за собой представление о распространении света во времени, между тем Ферма считал распространение света мгновенным. Это осложнение не укрылось от математика Ферма, однако он предполагал, что возможно преодолеть его. считая распространение мгновенным и объясняя сопротивле ние «антипатией» света к веществу, постулированной также де л а Шамбром. По-видимому, Ферма сам не был удовлетворен такой уверткой. Мы будем, вероятно, ближе к действительности, если предположим, что его уму математика проблема представлялась в чисто геометрическом аспекте, который он пытался как-то связать с физической реальностью. Сама же проблема, канона сформулирована в том же письме к де ла Шамбру, заключается в следующем: дана точка А в полуплоскости, определяемой прямой BD (и точкой А), и точка С на противоположной полуплоскости, и дан коэффициент m, отличный от единицы; требуется на прямой BD найти такую точку В, чтобы сумма АВ+m•BC была наименьшей из всех аналогично образуемых сумм.
В то время эту задачу решить было нелегко, но Ферма обещает своему другу дать решение, когда тот захочет: ведь Ферма был гасконцем, поясняет Декарт. Решения пришлось ждать четыре года, и, возможно, как многократно выяснялось при психологическом анализе научных открытий, оно неожиданно всплыло в сознании Ферма при попытке новой формулировки принципа экономии в природе: под кратчайшим путем следует теперь понимать уже не самый легкий, или самый простой, или путь с наименьшим сопротивлением, или с наименьшей антипатией, а путь, проходимый в кратчайшее время (breviori tempore percurri possint). Используя этот принцип в соединении с гипотезой о том, что скорость света постоянна в определенной среде и уменьшается с увеличением плотности среды, Ферма смог найти закон преломления и, к своему великому удивлению, установить, что он совпадает с законом Декарта. Формулировка принципа и его применение для доказательства закона преломления содержатся в отрывке под названием «Анализ преломления» (Ocuvres de Fermat, ed. P. Tannery et Ch. Henry, I, Paris, 1894, p. 170-172) из письма от 1 января 1662 г. к Кюро де ла Шамбру. Впоследствии в записке, названной «Синтез преломления», Ферма дает обратную теорему: если преломление света подчиняется закону Декарта и если показатель преломления равен отношению скоростей света в первой и во второй среде, то при распространении из одной среды в другую свет следует по пути, требующему наименьшего времени.
Новая формулировка принципа экономии требовала, естественно, конечной скорости света, не говоря уже о том, что он нарушался в известных случаях отражения от вогнутых зеркал. Последней трудности Ферма вообще не упоминает, полагая, по-видимому, что она решается с помощью рассуждения, которое мы приводили выше. Что касается конечной скорости распространения света, то Ферма считал, что можно обойти это понятке, поскольку его можно заменить (весьма неопределенными) «утечкой» или «сопротивлением» света, которые для разных сред различны, иначе говоря, чем-то, что можно рассматривать как словесное выражение его коэффициента т из чисто геометрической задачи. Ферма всегда сосредоточивал внимание больше на математической стороне задачи, чем на физической.
Против принципа Ферма тотчас ополчились картезианцы. Их главные возражения содержатся в одном из писем Клерселье (весьма резком, порой даже оскорбительном): принцип, согласно которому природа действует наиболее коротким или наиболее простым путем, не является физическим принципом, потому что он требует от природы сознательного поведения. Действительно, луч света, попавший на линию раздела двух сред, должен был бы знать, что, преломляясь данным определенным образом, он затратит наименьшее время. Кроме того, таким образом получилось бы, что время является причиной движения. Вариаций на эту тему можно было бы привести бесконечное множество. Приведя некоторые из них, Клерселье приходит к выводу, что Ферма показал, что преломление происходит так, «как если бы» свет шел по кратчайшему пути. Вначале физики тоже встретили новый принцип с недоверием. Пти не был доволен им. Гюйгенс в 1662 г. критиковал физические принципы, принятые Ферма, ни один из которых не достоверен, и особенно этот «злосчастный» принцип экономии, с помощью которого ничего нельзя доказать. Но очень скоро эти резкие суждения стали смягчаться. Уже через три месяца тот же Гюйгенс оценивал работу Ферма как весьма хорошую и тонкую, хотя считал ее физические основы весьма шаткими. Еще позже, повторив расчеты Ферма и убедившись в их правильности, Гюйгенс настолько поверил в этот принцип, или, как он его называл, в «феномен Ферма», что уверенно использовал в своей собственной теории равенство показателя преломления отношению скорости света в первой среде к его скорости во второй.
19. ДИФРАКЦИЯ
Всего лишь через несколько лет после установления закона преломления (Декарт) и его теоретического подтверждения (Ферма) было открыто другое явление отклонения света. Оно было описано в посмертно опубликованном труде Франческо Мариа Гримальди (1618-1663), человека необыкновенных способностей, исключительно трудолюбивого и желавшего верить лишь фактам, а не авторитету учителей, как уверяет он в предисловии к своей объемистой работе в 535 страниц, вышедшей в 1665 г. под названием «Physico-mathesis de lumine, coloribus et iride» («Физико-математический трактат о свете, цветах и радуге»).
Книга начинается с заявления об открытии нового типа отклонения света, названного Гримальди дифракцией - термином, сохранившимся в науке и по сей день.

Франческо Мариа Гримальди. Портрет кисти неизвестного автора
Открытие это было, несомненно, случайным и обязано тому обстоятельству, что Гримальди экспериментировал с очень тонкими пучками света, получающимися за маленьким отверстием в освещенном солнцем окне. В пучке света, проходящем через отверстие, ученый помещал предмет и получал его тень на белом экране. Он заметил, что на экране тень оказалась шире, чем должна была быть геометрическая тень, и, кроме того, по обе стороны от нее лежали три цветные полосы, синие с внутренней стороны по отношению к тени и красные с наружной. Далее, если этот световой пучок падает на непрозрачный экран со вторым маленьким отверстием, расположенный параллельно первому, и проходящий пучок наблюдается на еще одном экране, то получается центральное светлое пятно значительно большего размера, чем следует из геометрической оптики; края его окрашены в красный и голубой цвета. Не оставалось сомнения: за отверстием свет отклоняется.
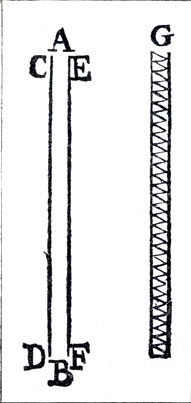
Схема светового луча по волновой теории Гримальди. (F. M. Grimaldi, De lumine, 1665.) Видно, что колебания предполагаются поперечными
После рассмотрения многочисленных вариантов эксперимента, выполнения многих других опытов по дифракции на тонких нитях, птичьих перьях, тканях, волокнистых веществах Гримальди пытается так объяснить это явление: как вокруг камня, брошенного в воду, образуются волны, так и препятствие, помещенное на пути пучка света, порождает в световом флюиде волны, отклоняющиеся за отверстием.
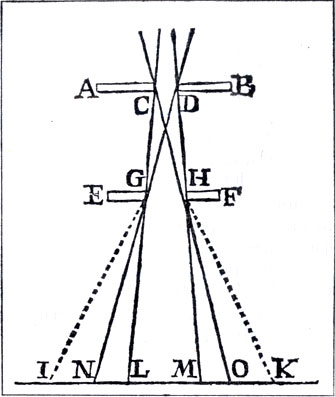
Опыт Гримальди по дифракции. (F. M. Grimaldi, De lumine, 1665.) Свет, входящий через отверстие CD в окне и проходящий отверстие GH в непрозрачной стенке, образует на экране световое пятно LM, окруженное цветными кольцами
Значит ли это, что для Гримальди свет является флюидом? Надо сказать, что его работа весьма интересна и курьезна. Интересна она своим содержанием, поскольку в ней рассматриваются самые разнообразные физические задачи (к одной из них мы еще вернемся). Курьезна же она тем, что в первой книге утверждается субстанциональность света, а во второй - его акцидентальность, или, пользуясь принятым Гримальди термином, более понятным для нас, - его волновой характер. К волновой гипотезе Гримальди прибегает, чтобы объяснить природу цветов, которые, как он говорит, являются составными частями света:
«Не исключена возможность, что видоизменения света, в силу которых он постоянно окрашивается в так называемые кажущиеся цвета, или, лучше сказать, становится видимым как цветной, представляют собой определенную его волнистость с очень частым волнением, как бы трепет распространения с мельчайшим волнением, благодаря которому и получается, что он действует на орган зрения определенным характерным для него образом» (F. M. Grimаldi, Physico-mathesis de lumine, Bononiae, 1665, p. 342).
В поддержку этой своей волновой теории Гримальди приводит целый ряд аргументов, и в частности аналогию со звуком, различная высота которого, как учил Галилей, зависит от различных колебаний воздуха. Можно сказать, что Гримальди закончил начатый Декартом и происходивший не без сильного сопротивления процесс перенесения цветов в область физических явлений.
Опыты, аналогичные опытам Гримальди, в 1672 г. провел Роберт Гук, причем утверждал, что провел их независимо. Однако хорошо известен крупный недостаток характера Гука, заключающийся в том, что он всегда заявлял о своем приоритете на чужие изобретения. Во всяком случае, опыты Гука ничего не добавили к опытам Гримальди.
Совсем иное значение имеют опыты Гука, описанные в его «Micrographia» («Микрографии»), вышедшей в 1665 г., в том же году, в котором вышел «Физико-математический трактат» Гримальди. «Микрография» - очень интересная книга, особенно для истории микроскопа, сконструированного еще Галилеем и использованного Гуком с исключительным искусством. Среди его микроскопических наблюдений заслуживают особого упоминания наблюдения тонких слоев (мыльные пузыри, масляные пленки и т.п.) помещаемых в световой пучок. Гук заметил их окрашивание, внимательно исследовал его и пытался объяснить с помощью «колебательной» теории света, на которой мы не будем останавливаться, поскольку она не представляет особого интересса.
20. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ И СКОРОСТЬ СВЕТА
Прежде чем рассмотреть в следующей главе две основные теории света, которые в течение нескольких веков с переменным успехом вели спор друг с другом, следует еще упомянуть о двух открытиях, предшествовавших этим теориям и оказавших на них влияние.
В 1669 г. датчанин Эразм Бартолин (1635-1698) опубликовал работу под названием «Experimenta crystalli islandici disdiaclastici, quibus mira et insolita refractio detegitur» («Опыты с кристаллами исландского известкового шпата, которые обнаруживают удивительное и странное преломление»). Он описывает опыты с исландским шпатом, в которых он обнаружил «удивительное и странное» двойное лучепреломление. Как известно, речь идет о следующем: если луч света попадает на поверхность исландского шпата, он, преломляясь, раздваивается. Бартолин, кроме того, заметил, что один из двух лучей подчиняется закону преломления Декарта с показателем преломления, равным 5/3 по данным его измерений, тогда как второй луч, названный им «подвижным», а сейчас называющийся «необыкновенным», этому закону не подчиняется. Датский ученый открыл также, что в кристалле шпата существует направление, определенное им почти точно, вдоль которого луч не раздваивается. Бартолин приписал это явление распределению пор в кристалле. В дальнейшем (гл. 6) мы расскажем о гораздо менее наивном объяснении этого явления, которое дал Гюйгенс, проведший весьма точные исследования.
Несмотря на сомнения, высказанные Галилеем (см. гл. 4), Порта, Кеплер и Декарт продолжали считать скорость света бесконечной. Попытки итальянской Академии опытов определить скорость света методом Галилея, естественно, окончившиеся неудачей, о чем сообщается в «Очерках», еще более усилили убеждение в мгновенности распространения света, которое нельзя считать целиком предвзятым: большое значение имели приведенные Декартом соображения.
В 1672 г. астроном Жан Доминик Кассини (1625-1712), один из многих итальянских ученых, которые были приглашены в Париж Людовиком XIV, предпринял систематическое исследование спутников Юпитера. Он заметил определенные запаздывания в моментах вхождения первого спутника в конус тени планеты и выхода из нее, как если бы время обращения спутника вокруг Юпитера было больше, когда он находится дальше от Земли. А поскольку представлялось невероятным, чтобы время обращения спутников Юпитера зависело от расстояния до Земли, то этот астрономический факт представлялся необъяснимым.
Это явление было исследовано молодым датским ученым Олафом Рёмером (1644-1710), который пришел к выводу, что эту кажущуюся нерегулярность следует приписать конечности скорости распространения света. В сентябре 1676 г. он предсказал отставание, которое должно наблюдаться при предстоящем затмении первого спутника Юпитера в ноябре. Убедившись в правильности предсказания, он в том же месяце представил свою теорию Парижской Академии наук, утверждая, что свету требуется 22 минуты, чтобы пройти диаметр земной орбиты (более точное современное значение этой величины - 16 минут 36 секунд).
Однако в Парижской академии и в Парижском университете господствовала тогда картезианская философия, поэтому теория Рёмера встретила сильное сопротивление. Кассини, который сам принимал большое участие в наблюдениях, публично снял с себя ответственность за выводы Рёмера. Но все же нашлось много сторонников Рёмера как во Франции, так и особенно за рубежом; особенно важна была энергичная поддержка астронома Эдмонда Галлея.
Окончательно подтвердил теорию Рёмера и одновременно снял возражения Декарта астроном Бредли (1693-1762) в 1725 г., когда он, пытаясь найти параллакс некоторых звезд, обнаружил, что в своей кульминации они кажутся отклоненными к югу. Наблюдения, продолжавшиеся до 1728 г., показали, что в течение года эти звезды как бы описывают эллипс. Бредли интерпретировал это явление, названное в 1729 г. Евстахием Манфреди аберрацией, как результат сложения скорости света, идущего от звезды, скоростью орбитального движения Земли.
Хотя земные измерения скорости света были произведены лишь в следующем столетии (см. гл. 8), после Бредли конечность скорости распространения света была единодушно принята как опытный факт.
|
ПОИСК:
|
© NPLIT.RU, 2001-2021
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'