ВОКРУГ КВАНТА

ДУАЛИЗМ И НЕОПРЕДЕЛЕННОСТЬ

В волновой оптике давно знали, что ни в какой микроскоп нельзя разглядеть частицу, если ее размеры меньше, чем половина длины волны света, которым она освещена. В этом не видели ничего странного: волны света существуют сами по себе, частица — сама по себе. Но когда выяснилось, что частице тоже можно приписать длину волны, тогда это утверждение волновой оптики превратилось в соотношение неопределенностей: не может частица сама себя локализовать точнее, чем на половине длины своей же волны.

В пору становления квантовой механики даже хорошие физики с горечью шутили, что теперь им приходится по понедельникам, средам и пятницам представлять электрон частицей, а в остальные дни — волной.

Такой способ мышления приводил к множеству парадоксов, от которых мы будем избавлены, если сразу же заставив себя не разделять в электроне свойства «волна — частица». Только после этого соотношение неопределенностей Гейзенберга перестанет быть чем-то странным и превратится в простое следствие корпускулярно-волнового дуализма.

Чтобы убедиться в этом, поставим мысленный эксперимент по измерению импульса р летящей частицы с массой m. Как известно,

р = mv — поэтому нам достаточно измерить скорость v. Для этого нужно отметить ее положения x₁ и x₂ в моменты времени t₁ и t₂ и затем вычислить скорость по формуле:

v = (x₂ - x₁)/(t₂ - t₁) = Δх/Δt.

Как всегда при измерении, мы на частицу воздействуем и тем самым меняем ее скорость. Поэтому, если нам захочется измерить скорость v как можно точнее, мы должны выбирать точки х₁ и х₂ как можно ближе — перейти к пределу Δx -> 0. В классической физике так и поступают.

Но в квантовой механике мы не можем выбрать точки х₁ и х₂ как угодно близко, и все время должны помнить, что летящая частица — это не точка, а некоторый волновой процесс, и нельзя представлять ее меньшей, чем половина длины волны этого процесса. Поэтому погрешность δх определения каждой из координат х¹ и х₂ всегда будет больше или, в крайнем случае, равна λ/2.

По той же причине расстояние Δx = x₂ — x₁ между двумя последовательными измерениями нет смысла брать меньшим λ/2. Наиболее точное значение скорости v получается при значении Δх = λ/2, тогда оно будет равно v = Δx/Δt = λ/2Δt. Понятно, что даже это значение содержит неустранимую погрешность δv, которая зависит от точности δх определения координат х₁ и х₂ и равна

δv = (δх)/(Δt) ≥ (λ)/(2Δt).

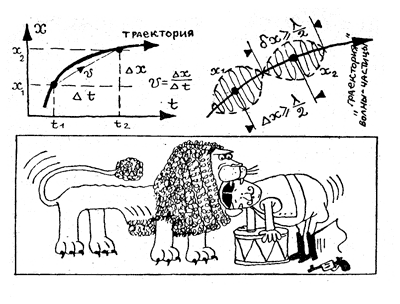
Дуализм

Сравнивая две последние формулы для v и Δv, приходим к неожиданному, но строгому результату: Δv > v . То есть погрешность определения импульса всегда больше или, по крайней мере, равна его наиболее точно измеренному значению: Δp ≥ p.

Абсолютная величина погрешности δр определяется длиной волны λ. В самом деле, формулу де Бройля λ = h/p можно обратить: р = h/λ. И поскольку δр ≥ р, то δр ≥ h/λ . Величина обеих погрешностей δx ≥ λ/2 и δp ≥ h/λ зависит от длины волны частицы λ. Чем медленнее движется частица, тем больше длина ее волны (λ = h/m v;) и тем меньше погрешность δр. Но как раз для такой частицы очень велика неопределенность координаты δх. Меняя скорость частицы, мы можем уменьшить либо δх, либо δр, но никогда не сможем уменьшить их произведение: δx • δp ≥ 1/2h