
Атом Бора
Вернемся, однако, к работам Бора о строении атомов. Бор, как и Томсон до него, ищет такое расположение электронов в атоме, которое объяснило бы его физические и химические свойства. Бор уже знает о модели Резер-форда и берет ее за основу. Ему известно также, что заряд ядра и число электронов в нем, равное числу единиц заряда, определяется местом элемента в периодической системе элементов Менделеева. Таким образом, это важный шаг в понимании физико-химических свойств элемента. Но остаются непонятными две вещи: необычайная устойчивость атомов, несовместимая с представлением о движении электронов по замкнутым орбитам, и происхождение их спектров, состоящих из вполне определенных линий. Такая определенность спектра, его ярко выраженная химическая индивидуальность, очевидно, как-то связана со структурой атома. Все это очень трудно совместить с универсальностью электрона, заряд и масса которого не зависят от природы атома, в состав которого они входят. Устойчивость атома в целом противоречит законам электродинамики, согласно которым электроны, совершая периодические движения, должны непрерывно излучать энергию и, теряя ее, «падать» на ядро. К тому же и характер движения электрона, объясняемый законами электродинамики, не может приводить к таким характерным линейчатым спектрам, которые наблюдаются на самом деле. Линии спектра группируются в серии, они сгущаются в коротковолновом «хвосте» серии, частоты линий соответствующих серий подчинены странным арифметическим законам.
Так, Иоганн Бальмер (1825-1898) в 1885 г. нашел, что четыре линии водорода На, Нр, Н7, Н5 имеют длины волн, которые могут быть выведены из одной формулы:
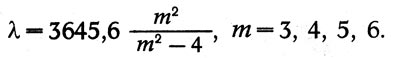
Позже было найдено еще два десятка линий в ультрафиолетовой части, и их длины волн также укладывались в формулу Бальмера.
Иоганн Ридберг (1854-1919) в 1889-1900 гг. нашел, что и линии спектров щелочных металлов могут быть распределены по сериям. Частоты линий каждой серии могут быть представлены в виде разности двух членов — термов. Так, для главной серии
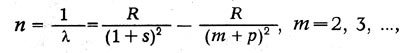
где R — некоторое постоянное число, получившее название постоянной Ридберга, s и р — дробные поправки, меняющиеся от серии к серии.
«Основным результатом тщательного анализа видимой серии линейчатых спектров и их взаимоотношений, — писал Бор, — было установление того факта, что частота v каждой линии спектра данного элемента может быть представлена с необыкновенной точностью формулой ν = Т — Т", где Т и Т" — какие-то два члена из множества спектральных термов Г, характеризующих элемент».
Бору удалось найти объяснение этого основного закона спектроскопии и вычислить постоянную Ридберга из таких фундаментальных величин, как заряд и масса электрона, скорость света и постоянная Планка. Но для этого ему пришлось ввести в физику атома представления, чуждые классической физике.
Это прежде всего представления о стационарных состояниях атомов, находясь в которых электрон не излучает, хотя и совершает периодическое движение по круговой орбите.
Для таких состояний момент импульса равен кратному от h/2n. При переходе с одной орбиты на другую электрон излучает и поглощает энергию, равную кванту. В заключительных замечаниях к трем своим статьям «О строении атомов и молекул» Бор формулирует свои основные гипотезы следующим образом:

«1. Испускание (или поглощение) энергии происходит не непрерывно, как это принимается в обычной электродинамике, а только при переходе системы из одного «стационарного» состояния в другое.
2. Динамическое равновесие системы в стационарных состояниях определяется обычными законами механики, тогда как для перехода системы между различными стационарными состояниями эти законы не действительны.
3. Испускаемое при переходе системы из одного стационарного состояния в другое излучение монохроматично, и соотношение между его частотой v и общим количеством излученной энергии Е дается равенством E = hv, где h — постоянная Планка.
4. Различные стационарные состояния простой системы, состоящей из вращающегося вокруг положительного ядра электрона, определяются из условия, что отношение между общей энергией, испущенной при образовании данной конфигурации, и числом оборотов электрона является целым кратным А/2 я . Предположение о том, что орбита электрона круговая, равнозначно требованию, что момент импульса вращающегося вокруг ядра электрона был бы целым кратным h /2л.
5. «Основное» состояние любой атомной системы, т. е. состояние, при котором излученная энергия максимальна, определяется из условия, чтобы момент импульса каждого электрона относительно центра его орбиты равнялся h/2n ».
Далее Бор пишет: «Было показано, что при этих предположениях с помощью модели атома Резерфорда можно объяснить законы Бальмера и Ридберга, связывающие частоты различных линий в линейчатом спектре».
Именно Бор получил для спектра водорода формулу:
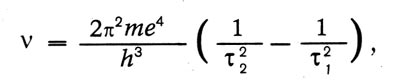
«Мы видим, — пишет Бор, — что это соотношение объясняет закономерность, связывающую линии спектра водорода. Если взять т2 — 2 и варьировать т1 получим обычную серию Бальмера.
Если взять τ 2 = 3, получим в инфракрасной области серию, которую наблюдал Пашен и еще ранее предсказал Ритц. При τ 2 = 1 и τ 2 — 4, 5,... получим в крайней ультрафиолетовой и соответственной крайней инфракрасной областях серии, которые еще не наблюдались, но существование которых можно предположить ».
Действительно, серия в ультрафиолетовой области, соответствующая τ 2= 1, была найдена Лайманом (1874— 1954) в 1916 г., серия в инфракрасной области, соответствующая τ 2 = 4, была найдена Брэкетом в 1922 г., и серия τ 2 — 5 была найдена Пфундом в 1924 г.
Используя известные в то время значения е, т, h, Бор вычислил значение постоянной в спектральной формуле:
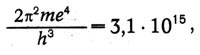
тогда как экспериментальное значение равно 3,290 • (10)15. «Соответствие между теоретическим и наблюдаемым значениями лежит в пределах ошибок измерений постоянных, входящих в теоретическую формулу», — писал Бор.
Бор дал объяснение спектральной серии, наблюдаемой в 1896—1897 гг. Пикерингом в спектре звезды ?-Кормы. Он показал, что эта серия соответствует спектру ионизированного гелия.
После опубликования статей Бора фаулер обнаружил новые линии при разряде в трубке, заполненной водородом и гелием, которые, по его мнению, не укладываются в серию Бора. Бор уточнил теорию, введя движение ядра и электрона около общего центра массы. Тогда:
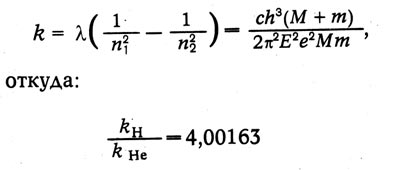
в точном соответствии с экспериментом.
В последующих работах Бор непрерывно уточнял основы своей теории. Она была дополнена принципом соответствия (1918), позволяющим делать определенные выводы об интенсивности и поляризации спектральных линий. Зоммерфельд развил теорию пространственного квантования, позволившую дать объяснение нормального эффекта Зеемана. Эффект Щтарка, открытый в 1913 г., был объяснен на основе модели Бора Эйнштейном и Шварцшильдом (1916). Сам Бор неоднократно занимался вопросом о влиянии магнитных и электрических полей на спектры атомов. Он же впервые включил в квантовую теорию атома и рассмотрение рентгеновских спектров, считая, что «характеристическое рентгеновское излучение испускается при возвращении системы в нормальное состояние, если каким-либо воздействием, например катодными лучами, были предварительно удалены электроны внутренних колец» (1913).
Волновой характер рентгеновского излучения был установлен Максом Лауэ (1879-1960), Вальтером Фридрихом (1883—1968) и Паулем Книппингом (1883-1935). В 1912 г. Лауэ пришла в голову мысль использовать в качестве дифракционной решетки для рентгеновских лучей кристалл. Он предложил Фридриху и Книппингу произвести эксперимент. Эксперимент с кристаллами цинковой обманки, каменной соли и свинцового блеска блестяще подтвердил предположение Лауэ. Статья Лауэ, Фридриха и Книппинга «Интерференционные явления в рентгеновских лучах» была опубликована в 1912 г. и в дополненном виде в 1913 г.
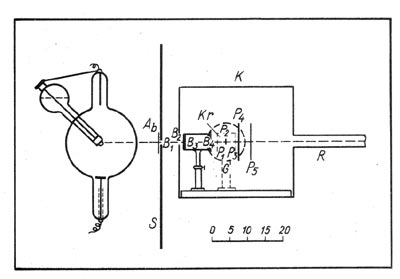
Рис. 70. Схема опыта Лауэ, Фридриха и Книппинга
Лауэ сразу же после опытов Фридриха и Книппинга дал теорию эксперимента, которая составила первую теоретическую часть статьи 1913 г. Однако она еще не давала возможностей точного измерения длин волн рентгеновских лучей, поскольку не была известна точно структура кристаллов. Основы рентгеноскопии и рентгеноструктурного анализа были даны отцом и сыном Брэггами: Вильямом Генри Брэггом (1862—1942) и его сыном Вильямом Лауренсом Брэггом (1890-1971). Они нашли, что пучок рентгеновских лучей отражается от поверхности кристалла по закону геометрической оптики для углов скольжения Θ, удовлетворяющих условию:
2dsinΘ = nλ.
Аналогичное соотношение было найдено русским физиком Юрием (Георгием) Викторовичем Вульфом (1863—1925). Закон Брэггов и Вульфа дал возможность измерить длины рентгеновских лучей.
Открытые в 1908 г. Чарлзом Гловером Баркла (1877—1944) так называемые характеристические лучи образуют линейчатый спектр, распадающийся на серии, обозначаемые в рентгеноскопии буквами К, L, M, N, ... .
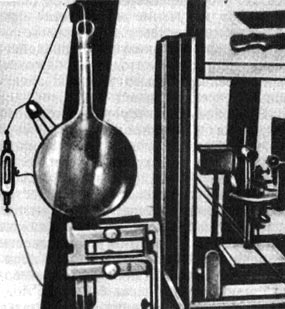
Рис. 71. Установка Лауэ, Фридриха и Книппинга
Генри Мозли в 1913—1914 гг. открыл закон смещения длин волн характеристических лучей, принадлежащих к одной и той же серии, при переходе от элемента к элементу. Частота рентгеновских лучей, определяющая их «жесткость», возрастает с возрастанием порядкового номера элемента. Заметим, что пионеры рентгеноскопии М. Лауэ, В. Г. и В. Л. Брэгги, Ч. Баркла получили Нобелевские премии по физике: Лауэ — в 1914 г., Брэгги —в 1915 г., Баркла — в 1917 г.
Первое теоретическое истолкование рентгеновских спектров на основе идей Бора состоит в том, что они обязаны переходам электронов на вакантные места во внутренних оболочках. Оно было дано Зоммерфельдом в его фундаментальной работе 1916 г. В том же 1916 г. П. Дебай и П. Шеррер разработали новую методику рентгеновского анализа кристаллов в порошке, получившую широкое распространение в рентгеноструктурном анализе.
Идеи Бора получили экспериментальное подтверждение в опытах Джеймса франка (1882—1964) и Густава Герца, которые начиная с 1913 г. изучали соударения электронов с атомами паров и газов. Оказалось, что электрон может сталкиваться с атомами газов упруго и неупруго. При упругом ударе электрон отскакивает от тяжелого атома (например, ртути), не теряя энергии, при неупругом ударе его энергия теряется и передается атому, который при этом либо возбуждается, либо ионизируется. Порции энергии, затрачиваемые на возбуждение атома, вполне определенные: так, электрон при столкновении с атомами ртути теряет энергию 4,9 эВ, что соответствует энергии кванта ультрафиолетового света длиной волны 2537 А. Квантовый характер поглощения энергии атомом был продемонстрирован в опытах франка, Герца и других физиков с поразительной наглядностью. За эти исследования, которые продолжались ряд лет, в 1925 г. франк и Герц были удостоены Нобелевской премии.
Квантовый характер излучения и поглощения энергии атомом лег в основу теоретического исследования о световых квантах, выполненного Эйнштейном в 1916—1917 гг. В этом исследовании Эйнштейн вывел формулу Планка, исходя из представления о направленном излучении. Атом излучает и поглощает энергию квантами. Выстреливая квант в определенном направлении, атом сообщает ему не только энергию hν , но и импульс hν/c. При излучении молекула газа переходит из энергетического состояния Zmc энергией em в состояние Zn с энергией еn излучая энергию еm — еn. Поглощая такую же энергию, молекула переходит из состояния Zn в состояние Zm Молекула может перейти из состояния Zm в состояние Zn самопроизвольно, спонтанно. Вероятность такого перехода за время dt пропорциональна этому промежутку времени dt:
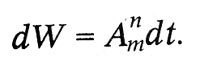
Но, кроме этого спонтанного перехода, впервые введенного Бором при объяснении спектров, по Эйнштейну, для молекул и атомов, находящихся в световом поле, возможны индуцированные переходы под действием светового излучения. Вероятность такого «индуцированного излучения»:

где ρ — объемная плотность световой энергии. Точно так же вероятность поглощения энергии молекулой, находящейся в состоянии Zn и перехода ее на высший энергетический уровень Zm, будет:
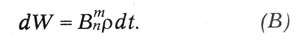
В равновесном состоянии атом в среднем столько же поглощает энергии, сколько и излучает. Поэтому:
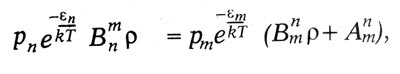
где по закону статистики Больцмана число молекул, находящихся в состоянии Zn, пропорционально:
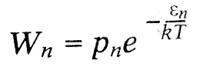
Из предыдущего равенства получается:
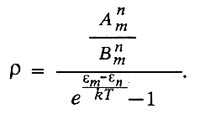
Положим εm - εn = hν, и для высоких частот, применяя закон Вина, получим формулу Планка:
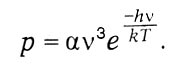
Идея Эйнштейна об индуцированном излучении нашла в современной физике и технике важное применение в лазерах.
Как было уже сказано, в 1916 т. Зоммерфельд обобщил теорию Бора, введя правила квантования для систем с несколькими степенями свободы. Он рассмотрел движение по эллипсу, введя азимутальные и радиальные квантовые числа. Введя далее пространственное квантование и третье квантовое число, он дал теорию нормального эффекта Зеемана. Наконец, он дал теорию тонкой структуры спектральных линий и объяснение рентгеновских спектров. Все эти результаты были подробно разработаны им в классической монографии «Строение атомов и спектры», первое издание которой вышло в 1917 г. До 1924 г. включительно эта книга выдержала четыре издания. Последнее издание ее уже в двух томах вышло в 1951 г. и русский перевод — в 1956 г.

Таким образом, к 1917 г. идеи Бора получили всестороннее развитие как в работах самого Бора, так и других авторов. Они были экспериментально подтверждены, и теория Бора получила всеобщее признание. Но те трудные вопросы, которые были поставлены Резерфордом, еще не были сняты, а многие трудности, с которыми сталкивалась теория в попытках рассмотреть многоэлектронные атомы, аномальный эффект Зеемана и многое другое, показали, что в теории Бора при всех ее успехах есть серьезные недостатки принципиального характера. Трудности и противоречия накопились, и надо было искать выход. Но прежде чем рассказать, каким путем были преодолены трудности теории Бора, рассмотрим коротко историю развития физики в нашей стране.

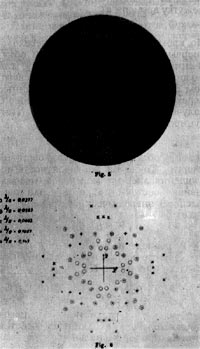
Рим. 72. одна из первых лауэграмм
|
ПОИСК:
|
© NPLIT.RU, 2001-2021
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'
При использовании материалов сайта активная ссылка обязательна:
http://nplit.ru/ 'Библиотека юного исследователя'